连分数

[拼音]：lianfenshu

[外文]：continued fraction

繁分数

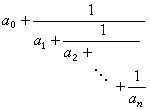
叫做有限连分数。常简记为[α₀，α₁，…，α_n]。当α₀是整数、α₁，…，α_n是正整数时，则叫做有限简单连分数，当n无限时，[α₀，α₁，…]称为无限简单连分数。通常连分数均指简单连分数。给定一有理数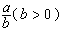，用熟知的辗转相除法，可展成有限连分数即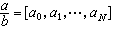，其中α₀，α₁，…，α_N是辗转相除法中依次得到的不完全商，规定α_N>1，则表法惟一。如果α是一个无理数，那么α可展成无限连分数，且表法惟一。反之，一有限连分数表一有理数，一无限连分数表一无理数。

渐近分数和完全商

在连分数[α₀，α₁，…，α_n，…]中取

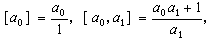
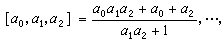
而写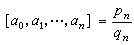，叫做连分数[α₀，α₁，…，α_n，…]的第n个渐近分数。 定义αń=[α_n，α_n+1，…]为连分数[α₀，α₁，…，α_n，…]的第n个完全商。

渐近分数有如下简单关系：

（1）

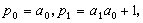
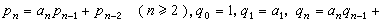
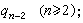
（2）

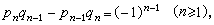
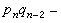
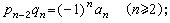
（3）(p_n，q_n)=1和q_n≥n (n≥2)

（4）

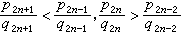
由此可得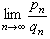存在；

（5）设α =[α₀，α₁，…，α_n，…]，n≥1，0<q≤q_n，且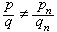，则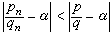，故在分母不大于q_n的诸分数中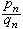， 与α最接近；

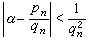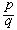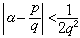（6）设α=[α₀，α₁，…，α_n，…]，则；反之，若有一个有理数适合，则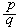必为α的某个渐近分数。

完全商有如下简单性质：

（1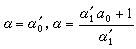），一般地，；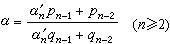

（2）α_n=[αń]，n=0，1，2，…，由此可推出实数展成连分数时表法惟一。该实数为有理数时，规定最后一个α_N>1。

循环连分数

设α=[α₀，α₁，…，α_n，…]，如果l≥m时，对某个固定的正整数k，有α_l=α_l+k，那么这样的连分数叫做循环连分数，这种最小的 k叫做它的周期，记为 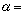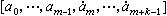。例如 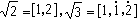等。运用渐近分数、完全商的性质以及抽屉原理，J.-L.拉格朗日证明了有关循环连分数的一个重要定理：一个连分数为循环连分数，则此数是某个有理系数的二次不可约多项式的根；反之亦然。

当D>0且不是平方数，则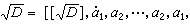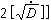，其中函数[x]表示不超过x的最大整数。此外，设佩尔方程x²-Dy²=1的最小解为ε，则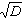的周期k满足。

应用举例

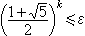连分数有许多应用。例如：

（1）1891年，A.胡尔维茨证明了：在α 的三个连续渐近分数中必有一个适合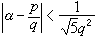。由此可得，任一无理数α，有无穷多个有理数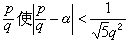。式中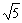是最佳的，即设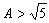，则必有一无理数α，使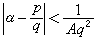不能有无穷多个解，如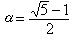就是这样一个数；

（2）设D>0且不是平方数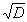，之连分数展开式中αń可表为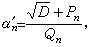，此处P_n及Q_n皆为整数。设n是最小的正整数，使(-1)^n-1Q_n=1，则x=p_n-1，y=q_n-1是佩尔方程x²-Dy²=1的最小解；

（3）利用连分数可以证明数论中一个著名的定理：设素数p呏1(mod4)，则p可表为二整数的平方和；

（4）在近似计算方面，如求多项式的根的近似值，等等。