[拼音]：tonglunlun
[外文]：homotopy theory
代数拓扑学的一个主要组成部分。它研究与连续映射的连续形变有关的各种课题。由于许多几何问题可以归结为同伦问题，然后谋求代数拓扑的解决办法，所以同伦论广泛地受到注意。
同伦的概念，直观上不难理解，同伦就是连续形变。以“形变收缩”为例，图
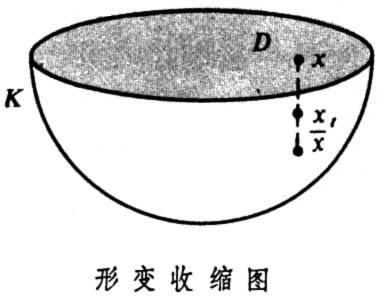
中的半球体K的边界包括半球面H与圆盘D。设想 K是由可以伸缩的质料构成，很显然，保持H上每个点不动，沿垂直于D的方向挤压K，最后可以将半球体K压成半球面H。也就是说，H是K的“形变收缩核”。这个形变收缩的过程可以描写得更确切一些。过K的任意点x垂直于圆盘D的直线与半球面H交于点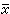
。对于0≤t≤1，令xt表示分线段x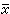为t:1－t之点。不妨认为挤压是从时刻t=0开始，到时刻t=1时完成，而时刻t时点x沿着线段x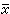到达xt的位置。使x对应于xt，定义了半球体K自身的一个连续映射ƒt:K→K，ƒt(x)=xt。于是，ƒ0(x)=x0-x。ƒ0为K自身的恒等映射，ƒ1(k)嶅H，并且ƒt(y)=y。当y∈H，ƒt就是一个“伦移”，使得K自身的恒等映射同伦于一个将K 映入子集H 的映射。
一般，设ƒ，g:x→Y为拓扑空间x到Y的两个连续映射。如果有连续映射H:x×I→x，I=[0，1]，使得h(x，0)=ƒ(x)，h(x，1)=g(x)，则称ƒ同伦于g，记作ƒ埍g。h是从ƒ到g的一个伦移，令ht(x)=h(x，t)，人们也说连续依赖于参数t的一族映射ht:X→Y是从ƒ到g的一个伦移。若伦移ht在x的某个子集A上是静止的，即h(x，t)=h(x，0)，0≤t≤1，则说 ƒ相对于 A同伦于g，记作ƒ埍g(relA)前一段举出的空间 H嶅K是空间K的形变收缩核，意思是指存在伦移h:K×I→K，使得对于x∈K有h(x，0)=x，h(x，1)∈H，而h(y，t)=y当y∈H，0≤t≤1。按照同伦关系埍，从x到Y的连续映射分成了同伦类。同伦类的集合记作[x，Y]。
在同伦论里，空间按同伦型而分类。若存在连续映射ƒ:x→Y，g:Y→x使得g。ƒ埍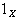
，ƒ。g埍1Y，则称x与Y具有相同的同伦型，则称ƒ(或g)为同伦等价，这里，1
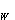:W→W表示空间W 的恒等自映射。若A为x的形变收缩核，则A与x有相同的同伦型。反之在不太强的限制之下，空间x与Y具有相同同伦型的必要与充分条件是它们可以一同放在一个空间Z里，使得x与Y都是Z的形变收缩核。
同伦论的典型问题大体上有下列几个，以下映射均指连续映射。
同伦问题对于给定的映射ƒ，g:x→Y，如何判断ƒ与g是否同伦？如果ƒ与常值映射同伦，则称ƒ为零伦的，记作ƒ埍0。如何判断给定映射ƒ是否零伦是这个典型问题的特例。
同调群提供了处理这个问题的工具。对任意整数n≥0，如果ƒ埍g，则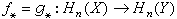
。因此，如果对某一n，ƒ
≠g，则ƒ与g一定不同伦。
但应注意，即使对所有n，ƒ=g，ƒ与g也未必同伦。H.霍普夫按下述方式作过一个映射ƒ:S3→S2，他把S3看成二维酉空间C2中的单位球面，把S2看成复射影直线，令ƒ是从S3到S2的自然投射，这个ƒ称为霍普夫映射，它不零伦但显然对所有n>0，ƒ=0:Hn(S3)→Hn(S2)。此例说明，要研究映射的同伦，除同调群以外，还需要别的工具。
设A嶅x，给定映射ƒ:A→Y能否扩张为x到Y的映射，即是否存在映射g:X→Y，使得
。
如果存在这样的映射g，则称g为ƒ 在x上的扩张，而ƒ为g在A上的限制，记作g│A=ƒ。恒同映射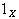
在A上的限制
称为A到x的内射。
一般说来，ƒ:A→Y不一定能扩张。例如，对n≥1，恒同映射
就不能扩张为Dn到Sn-1的映射g，因为如果这种g存在，则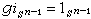
，由此得出
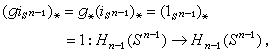
根据一些简单的计算，可以说明
因而
就不能成立。
很多重要的问题可以转化为映射扩张问题，1912年由L.E.J.布劳威尔首先提出的布劳威尔不动点定理就是典型一例。设 n≥0，ƒ:Dn→Dn是n维单位实心球体的自映射。则Dn中存在一点 x使得ƒ(x)=x。n=0时结论显然成立。设n>0，如果对任意x∈Dn，ƒ(x)≠x，则令g(x)是ƒ(x)到x的有向线段的延长线与Sn-1的交点，即得到映射
，使得
。根据前面所述，这不可能。因此Dn中至少有一点x使得ƒ(x)=x。
同伦问题实际上是扩张问题的一个特例。设ƒ，g：x→Y是映射，可定义映射G:x×0∪x×1→Y为
则ƒ与g是否同伦的问题成为G 能否扩张为映射F:x×I→Y的问题。
一般地称同伦映射所共有的性质为同伦性质，对于很多空间偶(x，A)(例如x是单纯复形，A是子复形)来说，ƒ:A→Y能否扩张成为x到Y的映射也是一个同伦性质。
提升问题在研究流形上有没有非零向量场时，需要考虑映射的提升问题，它与扩张问题相对偶。提法如下:设p:x→B与ƒ:Y→B是映射，是否存在映射g:Y→x，使得pg=ƒ:Y→B。如果存在这样的映射g，则称g为ƒ关于p的提升。是否存在g的问题就是提升问题。
又设p:x→B，愝:Y→x均为映射，ƒt:Y→B，0≤t≤1，是伦移，使得p愝=ƒ0。是否存在伦移
使得p愝t=ƒt(0≤t≤1)，且愝0=愝。如果存在上述愝t，则称愝t为ƒt的提升。寻找提升愝t，就是同伦提升问题。如果对任意空间Y及满足p愝=ƒ0的映射愝与同伦ƒt，总存在上述提升ƒt，则映射p:X→B称为具有绝对同伦提升性质，或称为纤维化。它是纤维丛映射的推广，任何纤维丛映射都是纤维化。
同伦分类问题对于给定空间x与Y，如何由x与Y的已知的可计算的不变量去计算从x到Y的映射同伦类集合[x，Y]，这是代数拓扑学中经常碰到的问题，特别是同伦群的计算等。
如果x与Y满足一定的条件，则[x，Y]形成一个群。对n≥1及任意道路连通空间Y，W.赫维茨定义了πn(Y)=[Sn，Y]。可以证明πn(Y)是一个群，而且π1(x)就是庞加莱所定义的基本群。当n≥2，πn(Y)是交换群。从而把πn(Y)称为空间Y的n维同伦群，它也是同伦不变量。
近几十年代数拓扑学的发展表明，同伦群起着十分重要的作用。和同调群不同的是，对一般单纯复形来说，同调群可以计算，但如何计算同伦群却是一个至今远未解决的问题，即使对十分简单的n维球面Sn，当m相当大时，至今仍没有计算群πm(Sn)的办法。因此，同伦群的计算一直是代数拓扑学的重要课题。
如果π1(x)=0，则称空间x是单连通的。一般地，群π1(x)通过交换化所得的交换群恰是H1(x)。此外，赫维茨又研究了高维同伦群与同调群的关系。如果
，则πn(x)自然同构于Hn(x)，n≥2。反之，若
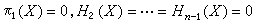，则也有同样结果。
关于球面同伦群的研究概况，首先要提出的是H.弗勒登塔尔的结果，他证明了
。
这个结果表明，当m小于2n－2时，πm(Sn)的构造仅与m-n有关，这就是球面同伦群的稳定性。
50年代初，J.P.塞尔提出了研究同伦群的新方法，他利用纤维化的谱序列，取得了球面同伦群计算的突破性进展。
关于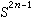
到Sn的映射α，H.霍普夫引进了一个霍普夫不变量，前面提到的霍普夫映射S3→S2的霍普夫不变量为1。J.F.亚当斯在20世纪 50年代末利用斯廷罗德运算提出了一个新的谱序列(以后称为亚当斯谱序列)，利用这个谱序列，他证明了只有当n=2，4，8时，才存在霍普夫不变量为1的映射。1960年以后，利用亚当斯谱序列，同伦群的研究又取得了重要的进展。不但πm(Sn)的计算有了很大的改进，而且，若干别的重要空间的同伦群计算也取得了不少成果。例如，某些托姆空间的同伦群（如协边群）也可以完全计算出来，这对于研究微分流形的分类具有重要意义。
扩张问题与同伦分类问题之间存在一定关系。这方面，S.艾伦伯格首先定义了阻碍上链与阻碍上同调类的概念。设K是任意单连通的单纯复形，n是正整数，K
表示K中所有维数不大于n 的单形组成的子复形（称为K的n维骨架）。设ƒ:K→Y为任给映射，σ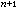
为K上任意n+1维单形。则σ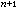的边界 嬠σ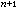可以看成一个n维球面，因此，
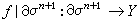代表 πn(Y)的一个元素，记作
。然后定义上链
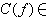
为
，
<C(ƒ)，σ
>表示上链C(ƒ)在σ上的值。不难证明：
（1）ƒ可扩张为K()到Y的映射匔C(ƒ)=0；
（2）δC(ƒ)=0。因此就称C(ƒ)为ƒ的阻碍上链，而称[C(ƒ)]∈H(K;πn(Y))为ƒ的阻碍上同调类。阻碍类为0，标志着ƒ｜K(n-1)可以扩张到K()上。
若π为群，n为正整数，当n>1时，还假定π为交换群。如果道路连通空间Y满足条件
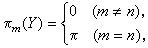
则Y称为艾伦伯格-麦克莱恩空间，记作K(π，n)。可以证明，对同一个π和同一个n，K(π，n)的伦型在一些不强的限制下是惟一的。利用上述阻碍上同调类可以证明：对任意交换群π及单纯复形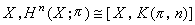
。
普通同调群满足七个公理，满足维数公理（m>dim X时，Hm(x)＝0）以外的六个公理的函子称为广义同调论。现在已经出现了许多有意义的广义同调论。例如，对研究向量丛有重要意义的K-同调论K*；对研究微分流形有重要意义的协边同调群MU*；对研究球面同伦群有重要意义的BP同调群BP*。E.布朗在 20世纪60年代初就已经证明，只要广义上同调函子还满足一定的条件，则这个广义上同调群就自然同构于空间到一个固定空间（或空间谱）的所有映射同伦类所成的群。例如K*(x)=[x，BU]，MU(x)=[x，MU]，其中BU表示U群的分类空间；MU表示BU 的托姆空间。上面的结果说明同调论的问题又可以转化为同伦论的问题。代数拓扑学的这两个主要分支就统一起来了。
伦型问题M.M.波斯尼科夫利用阻碍上同调类引进了一组能确定许多空间伦型的同伦不变量。设 x为一个单连通胞腔复形，对任意正整数n;可以作胞腔复形xn与映射ƒn:x→xn，使得：
（1）
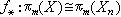，当m≤n。
（2）
，事实上，可以取xn为
加上一些维数大于等于n+2的胞腔使得所有维数大于等于n+1的同伦群等于零所得的空间。因此，不妨假定
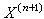，映射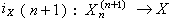
的阻碍上同调类
称为x的波斯尼科夫不变量。波斯尼科夫证明了:x的所有同伦群与所有波斯特尼科夫不变量能够确定x的伦型。应当指出，波斯尼科夫不变量的计算是以同伦群为基础的更为复杂的问题。