[拼音]：jiaohuanhuan
[外文]：commutative ring
乘法适合交换律的环。对交换环只有“理想”、“零化子”、“零因子”、“极小（大）条件”等定义，而不区分“左”“右”。无零因子的交换环叫做整环。数环与域F上的多项式环F[x]都是整环。整环不一定有单位元素，如偶数环。整环上的多项式环仍为整环。
设R为有正则元的交换环。如果S是R中一些正则元作成的乘法封闭集合(即S中任二元素之积仍在S中)，那么R可扩张成一个有单位元素的交换环
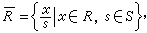
叫做R关于S的分式环，使S的元素在垪中恒有逆元素。特别地，当S为R中所有正则元作成的子集时（此时S自然地成为乘法封闭集合），垪 就简称为R的分式环。又如果R是整环，那么R的分式环必为域，特称为R的分式域(或商域)。如整数环的分式域便是有理数域。
局部化
设R是一个有单位元素e的交换环。它一定含有极大理想。所谓极大理想，是指R的一个理想N，满足条件:N<R，且N与R之间不能再介入R的其他理想。R的一个理想N是极大理想，必要而且只要，剩余类环R/N是域。当R只含一个极大理想时，就称之为局部环；当R只含有限多个极大理想时，就称之为半局部环。设P是R的一个质理想，S是P在R中的余集，在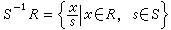
中视
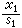与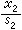
为同一元素，必要而且只要，有
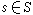使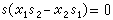
。于是可把S-1R定义成一个交换环，特记为Rp，并称为R在P处的局部化。它是局部环并以PRp为惟一的极大理想。如果对每个环R来说，R具有某个性质，必要而且只要对R的每个质理想P，Rp恒具有该性质，那么环的该性质称为局部性质。若要检验某环R是否具有某个局部性质，则只要检验每个Rp即可。由于Rp比R的结构简单，因此由局部特性来掌握整体特性是一个有效的手段。
高斯环
若R中有α=bс，则b称为α的一个因子，自然，с也是α的一个因子。或者α称为b的倍元，也称为b整除α，记为b|α。显然单位元素e是任意元素的因子，零元素θ是任意元素的倍元。R中一个有逆元素的元素，也称为R中的一个单位。例如，单位元素e就是一个单位；在整数环中，1与－1是仅有的两个单位;在多项式环F[x]中，一个元素为单位，必要而且只要，它是零次多项式（即域F中的非零元素）。环R中两个非零元素α与b如果能互相整除，即α｜b且b|α，那么就说α与b相通。两个非零元素α与b是相通的，必要而且只要，有R中的单位δ使α=bδ。如果非零元素α=bс，且b与с均非单位，那么就说b是α的一个真因子（自然，с也是α的一个真因子）。如果非零元素α不是单位，且无真因子，那么就说α是一个不可约元素。如果非零元素p不是单位，且具有“当p｜αb时，必有p|α或p|b”之性质，那么就说p是一个质元素。R中的质元素恒为不可约元素，但是反过来说就未必正确。例如在数环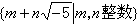
中，2是不可约元素但非质元素，因有
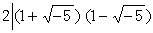，而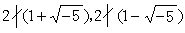 
。环R中的元素с若既是α的因子又是b的因子，则с称为α与b的一个公因子。如果α与b的一个公因子d具有“α与b的任意公因子恒为d的因子”之性质，那么就说d是α与b的一个最高公因子。一般说来，两个元素未必有最高公因子。例如在上述的环中，6与（
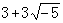）就没有最高公因子。所谓高斯环或惟一分解整环，是指有e的整环R，其中每个非单位α≠θ均可惟一地分解成一些质元素pi的乘积。所谓惟一性，意即若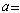
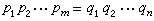，其中诸pi与qj均为质元素，则必m=n，且可排因子的次序使pi与qi相通(i=1，2，…，n)。有e的整环R是高斯环，必要而且只要满足下列条件①与②或①与③：
（1）R中真因子的降链α1，α2，…必止于有限处，即从任意非零非单位α1开始，若α1有真因子α2，α2又有真因子α3，如此下去，到某步必得出一个不可约元素，设其为αn，于是真因子的降链α1，α2，…即到αn为止。
（2）R中的不可约元素恒为质元素。
（3）R中任意两个不全为零的元素恒有最高公因子。
若R为高斯环，则R[x]亦然。于是域F上的多项式环F[x1，x2，…，xn]恒为高斯环。如果有e的整环R的理想恒为主理想(即由一个元素生成的理想)，那么就说R是一个主理想环。有e的整环R是一个主理想环，必要而且只要满足上述条件①与如下的条件④:R中任意不全为零的α、b恒有一个形式上为αs+bt的最高公因子。因此，主理想环恒为高斯环，但是反之则未必然。设R为有e的整环。如果对R中每个非零元α，恒有非负整数‖α‖与之相应，并对R中任意α，b(α≠θ)，恒有q、r∈R使 b=qα+r，且r=θ或者‖r‖<‖α‖，那么就说R是一个欧氏环。欧氏环恒为主理想环，但是反之则未必然。整数环I为欧氏环，从而为主理想环，但是多项式环I[x]仅为高斯环，而非主理想环。
诺特环
一个交换环R的所有幂零元素构成R的一个理想K，称为R的克德根或幂零根。如果一个交换环除幂零元素外，不再含其他的零因子，便称为准整环。整环显然为准整环。设R是一个交换环。R的一个理想P为素理想，必要而且只要R/P为整环；R的一个理想Q叫做准素理想，如果R/Q为准整环;R的一个理想A叫做可分解的，如果有R的理想B、C，使A<B，A<C，A=B∩C，否则便说A是不可分解的；R的素理想恒为不可分解的；当R为诺特环（即其理想满足极大条件）时，R的不可分解的理想恒为准素理想，R的克德根必为幂零理想；当R为准整环时，R的克德根必为素理想。设Q为交换环R的任意一个准素理想，于是垪 =R/Q为准整环，其克德根噖为素理想，从而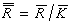
为整环。由R～垪，及垪～
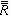易知，R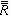～，设此同态映射之核为P，则由R/P≌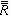知，P为R的一个含Q的素理想，它是由Q所惟一确定的，叫做与Q相伴的素理想，而Q则叫做属于P的一个准素理想。属于同一个素理想P的两个准素理想的交仍为属于P 的一个准素理想。由此便可引出诺特环中著名的交的惟一分解定理:在诺特环中，每个理想A均可分解为有限个准素理想Q1，Q2，…，Qr的交，使与诸Qi相伴的素理想Pi是彼此不同的，即此交不能够缩短，记为
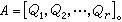又若A再分解为诸准素理想Q壟的不能够缩短的交
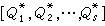，则必有r=s，且可排诸Q壟的次序使与Q壟相伴的素理想恰为Pi(i=1，2，…，r)。关于诺特环还有希尔伯特定理:如果R是有e的诺特环，则多项式环R[x]亦然。
（A.）E.诺特于1921年引进一般的满足极大条件的交换环而研究其理想论，这是由于代数几何的发展而需要研究多项式环的理想理论，后者的主要问题是判断一个多项式ƒ是否属于一个给定的理想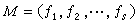
。此判断方法是通过把理想分解成准素分支而实现的。
维数
设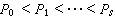
是环R中的素理想链，s称为此链的长度，R中所有的素理想链的长度的最大值（可能是无限）叫做R的维数，记为dimR。当R为诺特局部环以M为其惟一极大理想时，对每个属于M的准素理想Q，以δ(Q)表生成Q的最少元数，再以δ(R)表诸δ(Q)中的最小值，则有dimR =δ(R)。又若M恰可由δ(R)个元素生成，则称R为正则诺特局部环。
戴德金环
设R为有e的整环，F为其分式域，而且R<F(即R非域)。F的一个子集X如果满足：
（1）X是F作为加法群的一个子群；
（2）当α∈R，x∈X时，有αx∈X(即RX嶅X)；
（3）有β∈F，β≠θ使βX嶅R，则说X是R的一个分式理想。环R的理想显然均为R的分式理想，也可叫做R的整理想。F中的一个元素δ如果是R上首项系数为e(一般不写出来)的多项式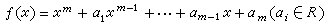 
的根，则说δ是R上的一个整元素。如果在F中，R上的整元素恒在R中，则说R是整闭的，如同R的两个整理想A、B可以相乘而得积AB仍为R的整理想一样，可以定义R的任意两个分式理想X与Y的乘法，而且积XY仍为R的一个分式理想。易知此乘法适合交换律与结合律，又R自己作为一个整理想（自然也是R的一个分式理想）与R的任何分式理想X相乘时，由于R有e，就恒有RX=X，故R的全部分式理想在乘法下构成一个有单位元素的交换半群，特别，其中所有非零分式理想又构成一个有单位元素的交换子半群。如果这个子半群还是一个子群，就说R容许理想理论。有e的整环R如果满足下列条件就叫做一个戴德金环:R的每个非零理想A恒可表为R的一些素理想Pi的乘积，A=
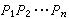，且除诸Pi的次序外，此表法是惟一的。
戴德金环的主要定理有两个。其一，有e的整环R为戴德金环，必要而且只要R满足下列三组等价条件之一：
（1）R容许理想理论。
（2）对R的非零(整)理想A、B只要A嶅B就有（整）理想C使A=BC;每个非零真（整）理想恒可惟一地表为有限个极大（整）理想之积。
（3）R为诺特环；R是整闭的；R 的非零素理想恒为极大理想。
其二，设R为有e的整环，F为其分式域，E为F的有限扩张（见域），Ω为E中所有在R上为整的元素作成的环。如果R为戴德金环，则Ω亦然。例如整数环R就是一个戴德金环。若E是有理数域F（即R的分式域）的一个有限扩张域，则E是一个代数数域，其中所有代数整数就组成一个环Ω，由于R是戴德金环，故Ω也是戴德金环。事实上。戴德金环的发生和发展就与代数数论有关，而且是从其中抽象出来的。
交换环是交换代数的主要研究对象。