[拼音]：fushu
[外文]：complex number
形如x+iy的数，其中x和y是实数，i是虚数单位（即满足关系i2=-1的数），也可记作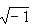
。
复数是16世纪人们在解二次、三次代数方程时引入的。在历史上，它们长期不为人们所接受，直到19世纪，才阐明了复数的概念，阐明了它们是从已知量确定出的数学实体。复数的一般形式是z=x+iy，其中x和y分别称为z的实部和虚部，记作x=Rez和y=Imz。如果Imz=0，那么 z=Rez是实数；如果Imz≠0，那么z称为虚数；如果Imz≠0而Rez=0，那么z称为纯虚数。两复数z1和z2相等就是其实部及虚部分别相等，记作z1=z2。
在平面上取直角坐标轴Ox和Oy，以坐标为(x，y)的点表示复数z=x+iy，于是Ox轴上的点表示实数，Oy轴上的点(z≠0)表示纯虚数（见图1
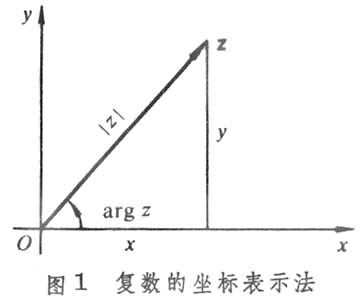
）。Ox轴和Oy轴分别称为实轴和虚轴；Oxy平面称为复平面，或者按表示复数的字母称它为z平面。
复数也可用在实轴及虚轴上的投影分别是x及y的向量表示，其起点可安放在平面上任一点，例如在原点。向量z=x+iy的长称为复数z的模，记作|z|，显然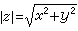
。实轴的正向与向量 z(z≠0)之间的夹角称为复数的辐角，记作Argz;Argz有无穷多个值，其中每两个相差2π的整数倍;在－π与+π之间的值称为Argz的主值，记作argz。于是z可用三角表示式表示为 z=|z|(cos Argz+isin Argz)，或记作
。
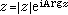设全体复数所构成的集为C 。复数的加法和乘法定义为
， 
，
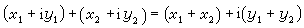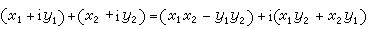式中x1，x2，y1，y2是实数。在C上引进这两种运算，不难证明它构成一个域，称为复数域。复数域C包含实数域R，但前者不是有序域，即任意两复数不能比较大小。
在复平面上，约定有一个无穷远点，以∞表示。加上无穷远点的复平面，称为扩充复平面。为了作出∞的几何表示，可把复数表示在球面上（见图2
）。
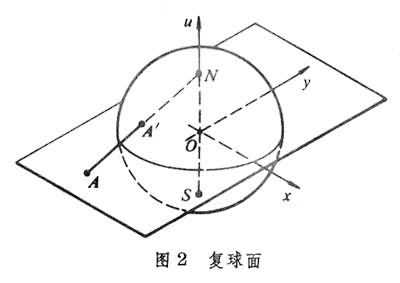
在点坐标是(x，y，u)的三维空间中，把Oxy平面看作就是z=x+iy平面。考虑球面
。
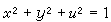取定球面上一点N(0，0，1)，称为球极，作连接N与Oxy平面上任一点A(x，y，0)的直线，并且设这直线与球面的另一交点是A┡，那么A┡称为A在球面上的球极射影。用它表示复数
z=x+iy。
如果点z的模愈大，那么它的球极射影愈接近N。约定N是无穷远点的球极射影，这样，在球面与扩充复平面之间建立了同构。这种球面称为复球面或黎曼球面。