[拼音]：gouzao luoji
[外文]：constructive logic
数理逻辑的一个分支，最典型的构造逻辑是直觉主义逻辑。下面以直觉主义逻辑作铨释。在经典数学中，对形如“扽xA(x)”命题的所谓存在性证明，只要求保证使命题A(x)成立的客体x存在即可，至于是否有方法保证找到（构造）这样的客体 x则可不论。但从构造的角度来看，就要求有方法保证找到（构造）使命题A(x)成立的客体x 才算证明成功。下面就是初等数学中非构造性证明的例子。
定理：存在两个无理数α与b使αъ是有理数。
证明：
不是有理数就是无理数。若 是有理数，则取
即满足定理；若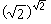
是无理数，则取
，
即满足定理。
类似这样的例子在经典数学中屡见不鲜。例如数学分析的“中值定理”，常微分方程中许多解的存在定理等。
进一步分析上述例子容易看出，无理数α与b存在性的这种非构造证明得以成功的依据在于使用了经典逻辑中的排中律，即认定“
不是有理数就是无理数”为真。因此，对待排中律的态度便成为区分经典逻辑与构造逻辑的主要标志之一。
比较能反映构造逻辑的一种形式系统是直觉主义谓词逻辑演算，它们又可被划分为三类：
（1）希尔伯特型系统；
（2）自然演绎型系统；
（3）序列演算。
在文献中，希尔伯特型系统比较常见。在这个系统中，排中律
不是一个逻辑公理，也不是这个系统中的可证命题，代之而使用较弱的逻辑公理：
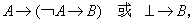
其中⊥是一个不可证命题。这条公理的逻辑意义是：矛盾可推出一切。在这个系统中有如下两条很重要的性质：
DP性质：
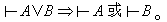
ED性质：
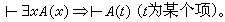
这两条性质正好反映了构造性证明的特征。
直觉主义谓词逻辑演算不是二值系统，它的完备性已经从不同角度被证明了，其中颇为有名的是S.克里普克给出的语义分析方法。在克里普克的语义分析中，论域D与D上的一个偏序≤共同组成一个全域〈D，≤〉，D中的元素称为时点，命题变元A在任一时点d∈D上被指派“真”或“假”值并记为(A)d，对复合命题的指派如下规定：
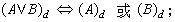
一个命题A在全域〈D，≤〉中为真是指该命题在这个全域的任何时点上都真。克里普克建立了下述完备性定理：一个命题是直觉主义逻辑系统的可证命题当且仅当它在任何一个全域中都是真的。
下面是K.哥德尔在1958年给出的希尔伯特型的直觉主义谓词演算系统：
设x是个体变元，t是项，A、B、C是公式，⊥为荒谬命题， 崊与匔为元数学记号（“由……得……”与“当且仅当”）。该系统由下述13条公理模式或推理规则组成：
