[拼音]：erciyu
[外文]：quadratic field
有理数域Q的二次扩域。每个二次域都可表示成
其中d 不等于1是无平方因子的有理整数，按照d>0和d<0，分别称K为实二次域和虚二次域。
二次域是除了有理数域之外最简单的一类代数数域。它有如下较简单的数学结构和特性：
（1）K的（代数）整数环为OK=Z[ω]，即K中每个（代数）整数均可写成α+bω，其中α、b∈Z，而
（当d呏2，3(mod4)时），
（当d呏1(mod4)时）。由此可知，K的判别式分别为d(K)=4d和d(K)=d。
（2）每个有理素数p在二次域K 中的分解规律为：对于p≥3时，若p｜d(K)，则p是 OK中一个素理想的平方（即p在K中分歧）；若p
d(K)，当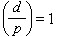
，则p为OK中两个不同素理想的乘积(即p在K中分裂)；当
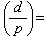-1，则p在OK中仍生成素理想(即p在K中惯性)。对于素数p=2，若 2｜d(K)，则 2在K中分歧；若2
d(K)，则必然d呏1(mod4)。当d呏1(mod8)时，2在K中分裂；当d呏5(mod8)时，2在K中惯性。
（3）二次域K 的单位根群记为WK。当
时，
；当 
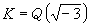时，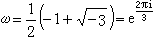
。而对于所有其他的二次域K，则WK={±1}。
（4）二次域K的单位群 UK，指的是整数环 OK中乘法可逆元全体。当 K为虚二次域时，UK=WK，而对于实二次域 K，存在一个单位 ε>1（称为 K的基本单位），使得
（5）二次域 
的（理想）类数hK也有简单的表达式：当d≤-5时，
（对于d=-1和-3，熟知hK=1）；当d>0时，
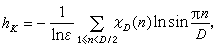
式中D＝｜d(K)｜;ε为基本单位；ln表自然对数；ⅹD是模D（惟一的）实本原特征。
1801年，C.F.高斯发表了他在20岁时所写的数论著作《算术研究》，展现了他的一个杰出的思想，即把有理数域和有理整数环上的许多初等数论问题，放到更大的域和环──二次域和它的(代数)整数环上来研究。他在这些方面的工作，是研究二次域的开端，也是代数数论的一个源头。
二次域有许多研究课题，其中最著名的是高斯关于类数问题的两个猜想：
（1）只有有限多个类数为1的虚二次域；
（2）存在着无限多个类数为1的实二次域。关于第一个猜想，1934年，H.海布雷恩证明了当d(K)→
时，hK→。1935年C.L.西格尔进一步证明了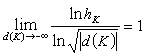
。A.贝克于1966年和H.M.斯塔尔克于1967年各自独立地证明了类数为1的虚二次域
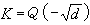只有9个：d=1，2，3，7，11，19，43，67，163。至于第二个猜想，则至今仍未解决。
- 参考书目
- D. B. Zagier，Zetaƒunktionen und Quadratische Krper，Springer-Verlag， Berlin， 1981.