[拼音]:Niudunfa
[外文]:Newton’s method
求非线性方程(组)零点的一种重要的迭代法,又称牛顿-拉弗森法或切线法。其要点是:若在非线性方程ƒ(x)=0的零点x=x*邻域内,函数 ƒ(x)连续可微且ƒ┡(x)不为零,xn(n=0,1,2,…)是x*的近似值,则在此邻域,用线性函数

近似代替ƒ(x),并以T(x)的零点

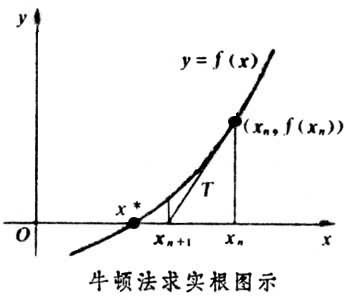
作为x*的新的近似值。这种通过构造序列x1,x2,…来近似x*的方法就是牛顿法。若ƒ(x)是实函数,x*是实数,则牛顿法有明确的几何意义:过点(xn,ƒ(xn))作曲线y =ƒ(x)的切线T,将T与x轴的交点xn+1作为x*的新近似值。对于非线性方程组,x和 ƒ(x)分别为矢变量和矢量函数,[ƒ┡(x)]-1为ƒ(x)的雅可比矩阵的逆矩阵。由牛顿法构造的序列x1,x2,…收敛于x*的充分条件是:
(1)在x*的邻域内ƒ┡(x)存在且满足李普希兹条件,即对x*邻域内的任意x┡、x″,有 ,式中0〈α〈1;
,式中0〈α〈1;
(2)[ƒ┡(x*)]-1存在;
(3)初始近似值x0充分接近x*。在上述条件下,x1,x2,…收敛于x*的速度不低于二阶。为了减弱收敛性对ƒ 的要求,提高收敛速度或减少计算量,牛顿法有许多变形,如修正牛顿法和拟牛顿法。