[拼音]：fei-Oujilide jihexue
[外文]：non-Euclidean geometry
不同于欧几里得几何学的几何体系，简称非欧几何。一般是指：罗巴切夫斯基几何（双曲几何）和黎曼的椭圆几何。它们与欧氏几何最主要的区别在于公理体系中采用了不同的平行公理。
历史渊源及发展
非欧几何的起源可追溯到人们对欧几里得平行公理的怀疑。从古希腊时代到公元1800年间，许多数学家都尝试根据欧几里得的其他公理去证明欧几里得平行公理，结果都归失败。19世纪，德国数学家C.F.高斯、俄国数学家Η.И.罗巴切夫斯基和匈牙利数学家J.波尔约等人各自独立地认识到这种证明是不可能的，也就是说平行公理是独立于其他公理的，并且可以用不同的“平行公理”替代欧几里得平行公理而建立非欧几何学。高斯关于非欧几何的信件和笔记在他生前一直没有公开发表，只是在1855年他去世后出版时才引起人们的注意。罗巴切夫斯基和波尔约分别在1830年前后发表了他们的关于非欧几何的理论。在这种新的非欧几何中，替代欧几里得平行公理的是罗巴切夫斯基平行公理：在一平面上，过已知直线外一点至少有两条直线与该直线共面而不相交。由此可以演绎出一系列全新的无矛盾的结论。在这种几何里，三角形内角和小于两直角。当时罗巴切夫斯基称这种几何学为虚几何学，后人又称为罗巴切夫斯基几何学，简称罗氏几何，也称双曲几何。
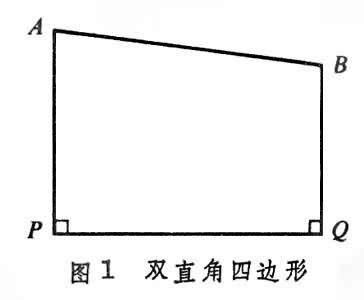
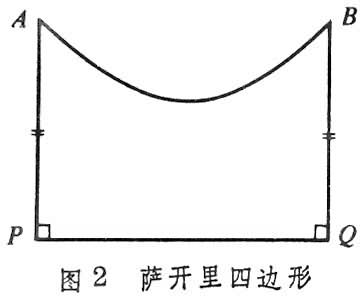
德国数学家D.希尔伯特于1899年发表了著名的《几何基础》一书，严密地建立了欧几里得几何的公理体系，它由五组公理组成，即结合公理、顺序公理、合同公理、平行公理及连续公理(见欧几里得几何学)。由结合公理、顺序公理、合同公理、连续公理四组公理所建立的体系称为绝对几何公理体系。绝对几何公理体系加上罗氏平行公理，就构成了罗巴切夫斯基几何的公理系统。绝对几何是欧氏几何与罗氏几何的公共部分，也就是说，绝对几何的全部公理和定理在两种几何里都成立。例如：命题“任意一个三角形内角和不能大于两个直角”；“在四边形PQBA中（图1），如果边PQ上的两个内角都是直角（此时称PQBA为双直角四边形）且边AP≥BQ，则∠A≤∠B，反之亦然。”等等，都是绝对几何里的定理。上述后一命题中的双直角四边形，若两边AP与BQ相等，则称之为萨开里四边形或等腰双直角四边形（图2），∠A、∠B称为萨开里四边形的上底角。于是命题：“萨开里四边形上底角不能大于直角”，也是绝对几何学的定理。这是非欧几何与欧氏几何的共同点，它们的不同点，就在于平行公理不同。
罗氏平行公理
它是欧氏平行公理（通过直线外一点只有一直线与已知直线共面不交）的否定命题，即：“通过直线外的每一点至少有两条直线与已知直线共面不交。”
罗氏几何的主要内容
罗氏几何里有许多不同于欧氏几何的定理，例如：
（1）共面不交的两直线，被第三直线所截同位角（或内错角）不一定相等(图3)。
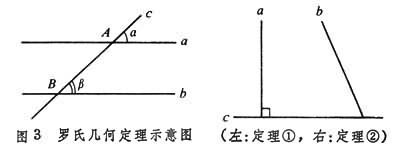
（2）同一直线的垂线和斜线不一定相交（图3右图）。
（3）三角形内角和小于二直角。
（4）两三角形若有三内角对应相等，则两三角形必全等（即不存在相似而不全等的三角形）。
（5）萨开里四边形上底角小于直角。这说明在罗氏平面上不存在矩形。
（6）通过不共线三点不一定能作一圆。
（7）三角形三条高线不一定相交于一点。
（8）通过直线 α外一点B 有无穷多直线与α共面不交，过 B也有无穷多直线与α相交（图4）。
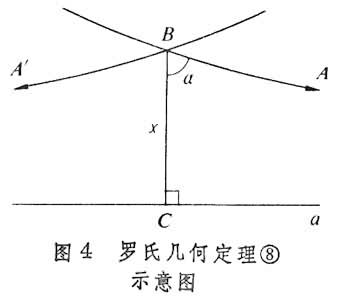
过点B作BC⊥α于C点，则在BC的一侧，在过B与α交与不交的两类直线中存在一条界线BA，它与α不相交，称之为直线α沿
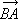方向的平行线，记作:在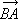方向上，
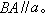在BC的另一侧也有：在
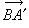方向上，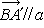
且过B点与α平行的直线恰此两条。称∠CBA为线段BC的平行角，线段BC为∠CBA的平行距或指针。设线段BC的长度d=x，∠CBA的角度μ＝α（图5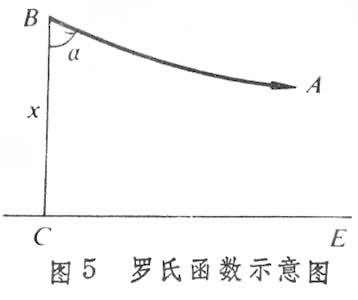
），则函数α＝π(x)称为罗巴切夫斯基函数，简称为罗氏函数。α=π(x)是单值单调递减函数，它可取尽0到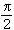
间的一切值，所以它是连续函数。这个函数用初等函数表示出来即是罗氏函数的解析表达式:π(x)=2arccote
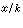，其中k是一个正常数。
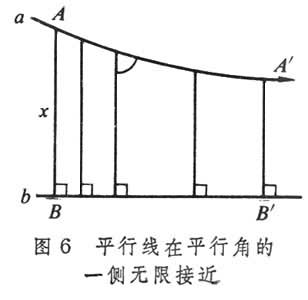
（9）在罗氏平面上两直线或相交或沿某方向平行，或既不相交又不沿任何方向平行，后者情况下，称为分散线或超平行线。任何两对平行线可以互相叠合。平行线α和b在平行角的一侧(平行方向)无限地接近（图 6），而在另一侧无限地远离。
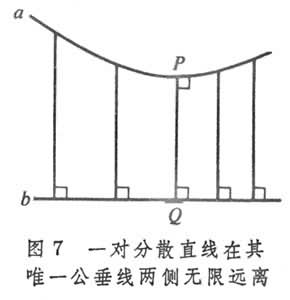
任何一对分散直线，有惟一的公垂线（图7），且沿此公垂线两侧它们无限地远离。
（10） 罗氏平面上下列三种直线的集合均称为线束。
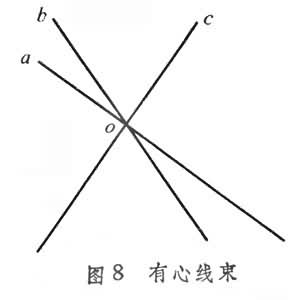
通过同一点O的一切直线的集合称为有心线束，点O称为其中心（图8）。
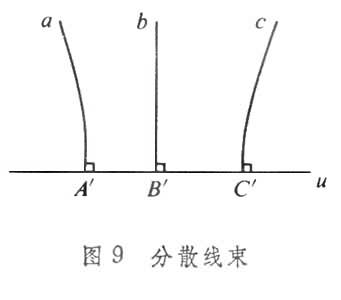
垂直于同一直线 u的一切直线的集合称为分散线束，u称其为底线（图9）
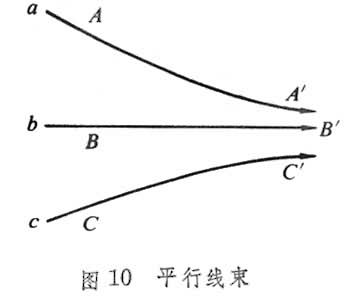
直线 AA┡以及平行此直线于方向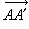
的一切直线的集合称为平行线束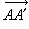，称为方向射线（图10）。
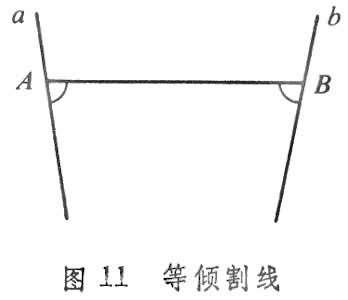
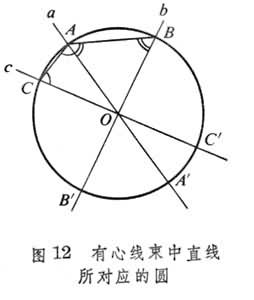
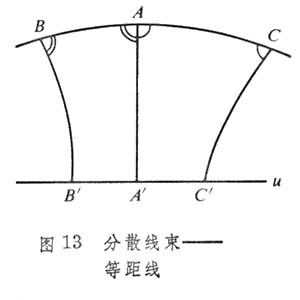
共面二直线α、b上各取一点A、B若AB截割此二直线所成的同侧二内角合同，则线段AB称为α、b二直线的等倾割线，而点A、B称为α、b的对应点(图11)。线束中一直线上已知点A及A在线束的直线上的一切对应点的集合是一条连续曲线，称为圆曲线（当线束有中心O时，点A关于O的对称点A┡也属此集合）。三种线束对应三种圆曲线:有心线束中一直线上点A及其对应点组成的圆曲线是以线束中心O为圆心，OA为半径的圆，记为⊙(O，OA) (图12)；分散线束上的点A及其对应点所组成的圆曲线上各点到底线u的距离相等，称之为等距线或超圆，记作⊙Г(u，A)（图13）；平行线束（方向射线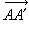
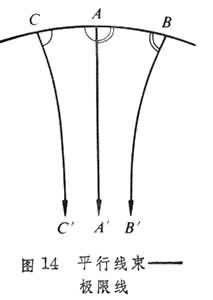
）上的点A 及其对应点组成的圆曲线是⊙(O，OA)。当O 沿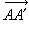无限远离A 时的极限位置，称之为极限线或拟圆，记作⊙Ω(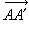，A)（图14）。
空间二直线的关系或是共面，或是异面。共面又有相交、平行、分散三种情况；异面即不在同一平面上。
一直线集合若包含两两共面但不全共面的一切直线称之为一个线把或线丛。空间线把有三种类型：
通过同一点O的一切直线称有心线把，O为其中心。
垂直于同一平面σ的一切直线称分散线把，σ为其底面（图15）。
平行于同一直线于方向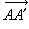
的一切直线称平行线把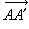，为其方向射线（图16）。
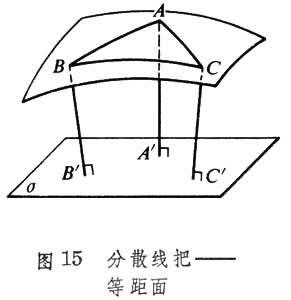
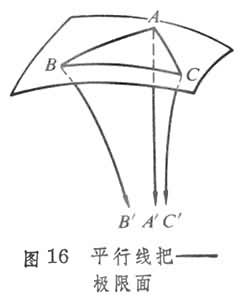
在一线把中，一直线上已知点A及A在线把中直线上一切对应点的集合称为球曲面（当线把有中心O时，A关于O的对称点A┡也属此集合）。线把为有心线把时，此球曲面即为以O为球心，OA为半径的球面；线把为分散线把时，此球曲面称为等距曲面或超球面；线把为平行线把时，此球曲面称为极限曲面或拟球面。
此外，在罗氏几何中还可以研究球曲面上的内在(内蕴)几何。极限曲面上的几何是欧氏几何;等距面上的几何是罗氏几何。
罗氏几何里有着与欧氏几何完全不同的刻画三角形边角关系的正弦定理和余弦定理。例如对于直角三角形来说，如果用A、B、C表示三内角，其C是直角，它们所对的边长分别为α、b、c，那么成立如下关系：
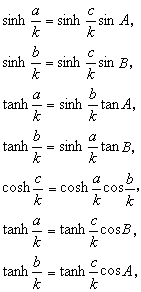
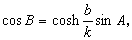
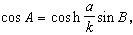
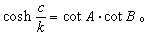
而对于斜三角形有正弦定理：
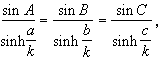
以及余弦定理:
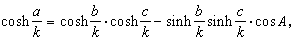
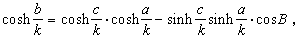
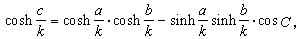
式中k是一个正常数，表示曲率半径；sinh、cosh、tanh、coth，分别是双曲正弦、双曲余弦、双曲正切、双曲余切。
利用上面这一套三角公式，同样地可以将非欧平面坐标化，然后用解析方法来研究各种非欧几何的问题，这就是非欧解析几何学。
椭圆几何
继罗氏几何后， 德国数学家 B.黎曼在1854年又提出了既不是欧氏几何又不是罗氏几何的新的非欧几何学。这种几何采用公理“同一平面上的任何两直线一定相交”代替欧几里得平行公理，并对欧氏几何中其余公理的一部分作了改动，在这种几何里，三角形内角和大于二直角。这种非欧几何学又称椭圆几何，它和球面几何学没有太大的差别，如果把球面的对顶点看成同一点，就得到这种几何学。
非欧几何的应用及发展
对于非欧几何的承认是在其创造者死后才获得的。意大利数学家E.贝尔特拉米在1866年的论著《非欧几何解释的尝试》一文中，证明了非欧平面几何(局部)实现在普通欧氏空间里，作为伪球面，即负常数高斯曲率的曲面上的内在几何，这样，非欧几何的相容性问题与欧氏几何相容性的事实就一样清晰明了。德国数学家F.克莱因在1871年首次认识到从射影几何中可推导出度量几何，并建立了非欧平面几何（整体）的模型。这样，非欧几何相容性问题就归结为欧氏几何的相容性问题，这些结果最终使非欧几何获得了普遍的承认。
非欧几何的创建打破了欧氏几何的一统天下，从根本上革新和拓广了人们对几何学观念的认识。1872年，克莱因从变换群的观点对各种几何学进行了分类，提出著名的埃尔朗根纲领，这个纲领对于几何学的进一步发展曾经发生重大影响。
非欧几何的创建导致人们对几何学基础的深入研究。希尔伯特于1899年建立了欧氏几何的公理体系。继几何学之后，数学家们又建立并研究了如算术、数理逻辑、概率论等一些数学学科的公理系统。这样形成的公理化方法已成为现代数学的重要方法之一。
非欧几何学的创建不仅推广了几何学观念，而且对于物理学在20世纪初期所发生的关于空间和时间的物理观念的改革也起了重大作用。非欧几何学首先提出了弯曲的空间，它为更广泛的黎曼几何的产生创造了前提，而黎曼几何后来成了爱因斯坦广义相对论的数学工具。A.爱因斯坦和他后继者在广义相对论的基础上研究了宇宙的结构。按照相对论的观点，宇宙结构的几何学不是欧几里得几何学而是接近于非欧几何学。许多人采用了非欧几何学作为宇宙的几何模型。
非欧几何学在数学的一些分支中有着重要的应用，它们互相渗透促进着各自的发展。H.庞加莱利用复平面上作出的罗巴切夫斯基几何模型证明了自导函数的基本区域是一些互相合同的多边形。这个结果对于建立自导函数理论有重要的作用。从一个已知的负常数高斯曲率曲面出发，可以通过经典的巴克伦德变换构造出新的负常数高斯曲率曲面，这个方法对于求解正弦戈登方程提供了从一个特解构造新的特解的有效方法。20世纪70年代以来，人们又注意到巴克伦德变换以及它的各种推广是研究一大类在物理上有重要作用的非线性偏微分方程的重要工具。