[拼音]：sanjiaoxue
[外文]：trigonometry
以研究平面三角形和球面三角形的边和角的关系为基础，达到测量上的应用为目的的一门学科。同时还研究三角函数的性质以及它的应用。
简史古代埃及人已有三角学知识，三角法主要是适应测量上的需要而产生的。例如，建筑金字塔，整理尼罗河泛滥后的耕地，以及通商航海，观测天象的需要。希腊的自然哲学家泰勒斯的相似理论，可以认为是三角学的萌芽，但历史上都认为希腊的天文学家喜帕恰斯是三角学的创始者。他著有三角学12卷，并作成弦表。
印度人从天文、测量的角度，曾研究过三角学，在公元6世纪，有阿耶波多第一也曾作出正弦表。中国唐代，瞿昙悉旺达在他所编的《开元占经》中曾介绍了印度的正弦表。
德国的J.雷格蒙塔努斯曾研究过天文学与三角学。在他的《论三角》一书中，有仿印度人的正弦表作成的非常精密的正、余弦表。他对天文、航海、测量方面都有很大的贡献。
16世纪法国著名数学家F.韦达的《应用于三角形的数学法则》，是他对三角法研究的第一本书，其中包括他对解直角三角形、斜三角形的一些贡献，例如有正切定理：
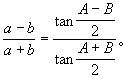
17世纪法国数学家棣莫弗也研究过三角问题。他曾发现有名的棣莫弗定理：
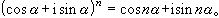
从17世纪后半期到18世纪，I.牛顿和丹尼尔第一·伯努利曾发现各种三角级数，例如
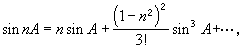
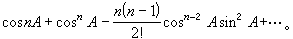
直到近代，才在三角学中引进现在使用的三角符号，并将三角法作为解析学的一部分，这是从L.欧拉开始的，欧拉曾发现：
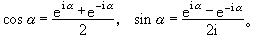
中国的戴煦在他所著的《外切密率》中，讨论了三角函数线与弧度之间的关系，并在他的《假数测图》中，结合三角函数与对数函数的幂级数阐明了三角函数对数表的作法。
三角函数在直角坐标系中，以原点O为顶点，射线Ox为始边，Op为终边的角为θ，设点p的坐标为(x，y)，距离｜Op｜=r，这时6个比
由角θ的大小确定，都是θ的函数，称它们为角θ 的三角函数（见图1
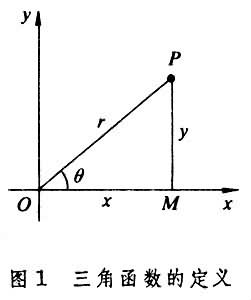
），分别记以下面的符号：
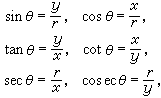
分别叫做角θ的正弦、余弦、正切、余切、正割、余割。
另外在中国古书中，又把1-cosθ、1-sinθ分别叫做正矢、余矢，用下面符号表示：
，
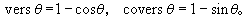因为一个角θ加以360°或2π弧度的整数倍，它的终边与角θ的终边相同，因此
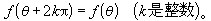
即三角函数是周期函数，以2π为周期。
如图2
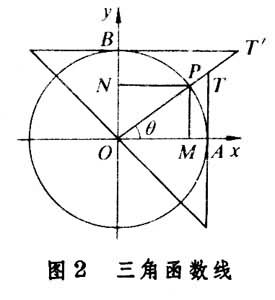
以O为圆心，以1为半径作单位圆。设它与x轴、y轴交于点A、B，∠AOp的终边与圆的切线AT、BT┡分别交于T、T┡，pM⊥Ox，pN⊥Oy。这时
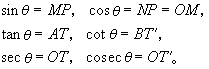
另外
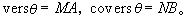
Mp、OM、AT、BT┡、OT、OT┡、MA、NB叫做三角函数线，中国古代把它叫做八线。因此，曾把三角法叫做八线学。
利用三角函数线，可以画出三角函数的曲线。例如，标准正弦曲线y＝sinx（如图3
）。
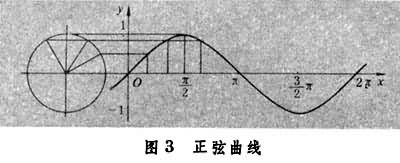
三角函数的基本公式有和角公式：
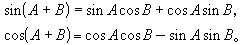
由此可以导出差角公式、倍角公式、半角公式以及和差化积与积化和差等公式。
如果θ表示弧度，对于θ的任意值，sinθ、cosθ可用下面的无穷级数表示：
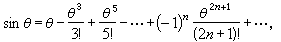
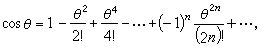
式中n!＝1×2×3×…×n。求某一角的正弦值和余弦值，可以按这些无穷级数求出，并且可以精确到任意小数位。
三角形的解法设平面三角形的三个角为A、B、C，它们的对边分别为α、b)、с，则有
正弦定理：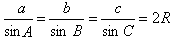
（R 为外接圆半径）；
余弦定理：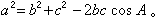
又设球面三角形的三个角为A、B、C，它们的对边分别为α、β、у，则有
正弦定理：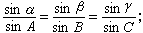
余弦定理：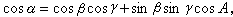
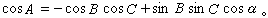
利用上述定理以及其他一些定理，可在已知三角形的某些元素（边或角）时求出其他未知元素。
反三角函数其定义如表所示：
三角方程
一般指含有某些三角函数的方程，这些三角函数的自变量中含有未知数。
适合于方程的一个未知数的实数值（可以理解为角的弧度数）叫做三角方程的一个解；适合于方程的未知数的实数值的集合叫做三角方程的通解。
形如sinx=α的方程叫做最简三角方程。它们的解分别是：
（1）sinx＝α
当｜α｜>1时无解。当α=1时通解为
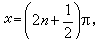
当α＝-1时通解为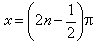
。当｜α｜<1时，通解为x＝nπ+(-1)narcsin α（n为整数）。
（2）cosx＝α
当｜α｜>1时无解。当α=1时通解为x=2nπ，当α=-1时通解为 x＝(2n+1)π。当｜α｜<1 时通解为x＝2nπ±arccosα（n为整数）。
（3）tan x＝α
通解为nπ+arctanα （n为整数）。
（4）cot x＝α
通解为nπ+arccotα （n为整数）。
一些特殊形式的三角方程可有精确解法。例如，形如ƒ（sinx，cosx，tanx，cotx）=0的方程，这里ƒ是有理函数，可用万能公式，令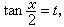
然后以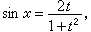
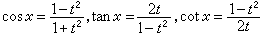代入原方程，即可得到关于t的有理方程。用这个方法，可以求出除了形如x＝(2n+1)π以外的方程的所有解。不能用精确解法来解的三角方程，可以用近似方法求解。