[拼音]：weifen liuxing
[外文]：differentiable manifold
一类重要的拓扑空间。它除了具有通常的拓扑结构外，还添上了微分结构。微分几何学的研究是建立在微分流形上的。三维欧氏空间R3中的曲面是二维的微分流形，但微分流形的概念远比这广泛得多，非但维数不限于二维，而且流形也不必作为n维欧氏空间Rn中的曲面来定义。此外，一般微分流形也不一定有距离的概念。
具体说来，设M是一个豪斯多夫拓扑空间。U是M的开集，h是U到n维欧氏空间Rn的开集(常取为单位球内部或立方体内部等等)上的一个同胚映射，则(U，h)称为一个坐标图，U称为其中点的一个坐标邻域。设M为开集系{Uα}所覆盖，即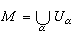
，则(Uα，hα)的集合称为M的一个坐标图册。如果M的坐标图册中任何两个坐标图都是Ck相关的，则称M有Ck微分结构，又称M为n维的Ck微分流形。Ck相关是指流形M上同一点的不同坐标之间的变换关系是Ck可微分的(k=0，1，…，∞或ω)，依通常记号Cw表示解析函数。具体来说， 如p∈Uα∩Uβ，(x
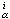)，(x
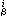)(i=1，…，n)分别是p在两个坐标图(Uα，hα)，(Uβ，hβ)下的(局部)坐标，即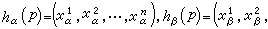
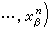那么它们之间的关系式可表为
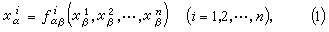
而ƒ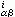
关于x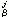
（j＝1，2，…，n）具有直到k次的连续导数。k=0时，M是拓扑流形；k>0时，就是微分流形；k=ω时，是解析流形。C∞流形又常称为光滑流形。
如果微分流形M是一个仿紧或紧致拓扑空间，则称M为仿紧或紧致微分流形。如果可选取坐标图册使微分流形M中各个坐标邻域之间的坐标变换的雅可比行列式都大于零，则称这个流形是可定向的。球面是可定向的，麦比乌斯带是不可定向的。
同一拓扑流形可以具有本质上不同的C∞微分结构。J.W.米尔诺对七维球面S7首先发现这个事实， 他证明七维球上可有多种微分结构。近年来，M.弗里得曼等得出如下的重要结果:四维欧氏空间中也有多种微分结构，这与 n(n≠4)维欧氏空间只有惟一的微分结构有着重大区别。
微分流形上可以定义可微函数、切向量、切向量场、各种张量场等对象并建立其上的分析学。以下的叙述对于Ck流形（k任意）也成立，但是，为了简单起见，仅就M为C∞流形来叙述。
可微函数设p∈U，ƒ是M上点p的邻域中定义的实值函数，(U，h)是C∞坐标图。如果函数ƒ。h-1：h(U)嶅Rn→R在h(p)点是r次连续可微的，则称ƒ在点p是Cr函数。这个定义与C∞坐标图的取法无关。如果在M上所定义的实值函数ƒ在M的各个点都是Cr的，则称ƒ为M上的Cr函数。M上的C∞函数全体组成一个实线性空间，记为F(M)。
切向量设p∈M，M在点p处的一个切向量是指从F（M）到R的一个线性映射x，使得对于任意的ƒ，g∈F(M)，满足：
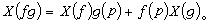
对于在p点的切向量x1，x2和实数λ1，λ2，定义λ1x1+λ2x2如下：
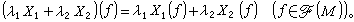
那么，点p处的切向量全体构成一个n维的实线性空间TP，TP称为在p处M的切空间或切向量空间(也记为TP(M))。如果（x1，x2，…，xn）为点p处的局部坐标系，则由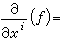
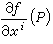定义的n个独立的切向量，构成TP的一组基，称为自然标架（或坐标标架）。M的切向量全体构成以M为底空间的向量丛（见纤维丛），称为M的切向量丛，简称切丛。M的切丛的一个截面称为M上的一个向量场。在局部坐标系中，向量场可表成
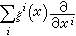
的形式，式中ξi(x)是坐标(x)i的C∞函数。
TP的对偶空间称为M在点p处的余切空间，记为T壩。T壩中的元素称为余切向量，也称协变向量。M的余切向量全体构成M的余切向量丛，简称余切丛，它的截面称为M上的一次微分形式。
由TP和T壩通过张量积的运算可以得到M在点p处的各种(r，s)型张量，M的(r，s)型的张量全体构成张量丛，它的截面就是M上的一个(r，s)型张量场（见多重线性代数、张量）。
可微映射设φ是从C∞流形M到C∞流形N 的连续映射，如果对于N上的任意Cr函数ƒ，M上的函数ƒ。φ总是Cr的，则称φ是Cr可微映射，或简称Cr映射。如果φ是从M到N上的同胚，而且φ和φ-1都是C∞的，则称φ为微分同胚，此时也称M与N是微分同胚的微分流形。
映射的微分设φ是从M到N的C∞映射。对M上点p的切向量x可以如下地定义N在点φ(p)处的切向量x┡：
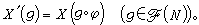
这个对应x→x┡用dφP表示，称为φ在点p处的微分。微分dφP是从切空间TP(M)到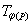
(N)的线性映射，有时也称为φ在切空间的诱导映射， 常用φ*P或φ*表示。利用对偶性，φ也自然地诱导了从余切空间T
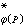到T壩的线性映射，常记为(dφP)*或φ壩或φ*。由张量积运算，φ还可以诱导对应点之间某些张量空间之间的线性映射。
设M和N是两个C∞流形，φ：M→N是C∞映射。如果微分dφP在M的每一点都是单射，则称φ是浸入，而φ(M)称为N 的浸入子流形。如果浸入φ还是单射，则称为嵌入，此时φ(M)称为N的嵌入子流形。
在微分流形上还可以定义外微分形式（见外微分形式）。p次外微分形式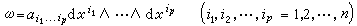
(2)是一些微分的外积的线性组合，这些微分的外积是反对称的，即
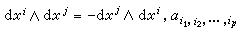是p阶反对称协变张量，M上p次外微分形式的全体构成一个实数域上的无限维向量空间Ep。对外微分形式可以进行加法运算（同次外微分形式可以相加），外积运算（p次外微分形式与q次外微分形式的外积是一个(p+q)次外微分形式），还可以进行外微分运算及积分运算。在局部坐标下，外微分运算为
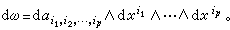(3)
设ω∈Ep且dω =0，则称ω为闭形式。M上p次闭形式的全体构成Ep的一个子空间记为Zp。设ω∈Ep，且ω=dσ(σ∈Ep-1，则称ω为正合形式。正合形式一定是闭形式。M上p次正合形式的全体也构成Ep的一个子空间记为Bp，Bp嶅Zp。商空间
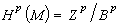(4)
称为p次德·拉姆上同调群(或p次上同调空间)。德·拉姆建立了微分结构与拓扑结构的一个重要关系：设M是紧致流形，则Hp(M)是有限维的，且其维数等于M的第p个贝蒂数bp。
仿紧微分流形均可赋予适当的黎曼度量（见黎曼几何学），且不是惟一的。有了黎曼度量，微分流形就有了丰富的几何内容，这时称为黎曼流形。黎曼流形是微分几何的主要的研究对象。