算术群

浏览

[拼音]：suanshuqun

[外文]：arithmetic group

李群中带有算术性质的一类离散子群。例如，实数域R中的整数全体Z；GL(n，R)中的GL(n， Z)；SL(n， R)中的SL(n，Z)等。令G=GL(n， R)，Г= GL(n，Z)，若GL(n，Q)的子群G′是与Г相称的，则G′称为GL(n，R)中的算术子群。所谓群H的子群H1与H2是相称的，意即H1∩H2在H1及H2中的指数[H1:H1∩H2]与[H2:H1∩H2]都是有限的。相称关系是个等价关系。设G是定义在有理数域Q上的线性代数群，GQ表G的Q有理点所成的子群， 又令GZ=GQ∩GL(n，Z)，若GQ的子群Г与GZ相称，则Г称为G的算术子群。这个性质是与G如何嵌入在GL(n，坴)中无关的。

如果Г 能同构于G 的一个算术子群， 则Г 称为算术群。显然，算术群中的有限指数的子群都是算术群。算术群是较为广泛的一种群，诸如有限群、有限生成的交换群、无挠的有限生成幂零群以及有限生成的非交换自由群都是算术群；如果环R又是有限秩自由Z 模，那么环R的所有单位所成的乘法群R+，都是算术群；特别地，代数数域K的整数环的乘法群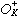，都是算术群。

还有一类重要的算术群。自然同态 ω：GL(n，Z)→GL(n，Z/qZ)下的核Kerω＝Гq，称主同余子群，这里ω是把任一n阶整系数方阵(gij)映射到方阵(ij)∈GL(n，Z/qZ)，其中q为大于1的正整数，而ij是整数gij所属的模q剩余类。含主同余子群Гq的算术子群Г，Гq嶅Г∩GL(n，Z)称同余子群。所以同余子群必然是算术子群，但是，每个算术子群Г是否都是同余子群，即是否有q使Г∩GL(n，Z)叾Гq，这是算术群理论中的一个核心问题，并称之为同余子群问题。当G＝SL(n，R)，n≥3时，同余子群问题已有肯定答案，而n=2时是否定的。对G是别的分裂型单连通单代数群时，也有类似结果。

最早研究的算术群是SL（2，Z），称为模群。设H是复数平面的上半平面，即H ={z=x+iy∈C│y>0}，矩阵以下列方式作用在H上:z ∈H，SL(2，Z)是SL(2， R)中的算术子群，对于这个算术子群SL(2，Z)可以找到H的一个子集D，使D是SL(2，Z)在H上的基本域，即满足①SL(2，Z)·D=H，②若g′∈SL(2，Z)，则集合{g∈SL(2，Z)｜gD∩g′D≠═}是有限集，也可以对一般算术群定义基本域。研究基本域的存在，紧致性、测度等方面的理论，称为算术群的简约理论。它也是算术群理论中的一个核心问题。早在19世纪，C.F.高斯和J.W.R.戴德金等人在研究椭圆函数的时候，就涉及模群SL(2， Z)及模群下不变的模函数，高斯在讨论正定二元二次型的整等价分类时，也已经知道模群的基本域。20世纪30年代C.L.西格尔研究算术群SL(n，Z)，并作出了它的基本域，称为西格尔区域，而SL(n，Z)称为西格尔模群。至于一般线性代数群中算术群的研究，则是在60年代由A.博雷尔、哈里什－钱德拉以及J.蒂茨开始。这个概念就是首先在他们研究李群中的格的存在性时产生的。随后，A.赛尔伯格和其他人提出了一个著名的猜想：R-秩大于2的任一半单李群的不可约格皆是算术的。经过博雷尔、M.拉格休内森等许多著名数学家的努力工作，这一猜想最后为G.A.马圭利斯所证实，他因此获得1978年的费尔兹奖。这些工作大大地推动和丰富了算术群的研究。

参考书目
  1. A.Borel，Introduction aux Groupes Arithméti-ques，Hermann， Paris. 1969.
  2. J.E.Humphreys，Arithmetic Groups，Lecture Notes in Math.789，Springer-Verlag， Berlin， 1980.
  3. M.S.Raghunathan，Discrete Subgroups of Lie Groups，Springer-Verlag， Berlin， 1972.
  4. G.A.Margulis，Arithmeticity of Irreducible lattices in Semi-Simple Groups of rank Greater Than 1，Mir.，Moscow， 1971.
阅读全文