[拼音]:ercixing
[外文]:quadratic form
线性代数的重要内容之一,它起源于几何学中二次曲线方程和二次曲面方程化为标准形问题的研究。二次型理论与域的特征有关。
若V是域F上的线性空间,q是从V到F的一个映射,使q(x)=φ(x,x),x∈V,式中φ是V上的对称双线性型,则q称为V上的二次型。当域F的特征不为2时,则φ由q惟一决定。此时φ(x,x)称为V上的二次型或二次齐式,而φ(x,y)称为此二次型的极型。若{e1,e2,…,en}为V的基底,则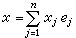 ,于是,二次型φ(x,x)可表为
,于是,二次型φ(x,x)可表为
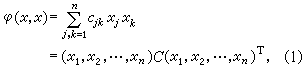
式中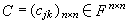 ,
,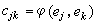 ,j,k=1,2,…,n。令
,j,k=1,2,…,n。令
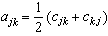 则
则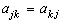 ,j,k=1,2,…,n。于是(1)可惟一地表为对称形式
,j,k=1,2,…,n。于是(1)可惟一地表为对称形式
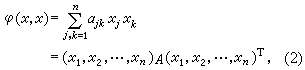
式中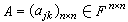 是对称矩阵,且称为二次型φ(x,x)在基底e1,e2,…,en之下的矩阵。A的秩rankA称为此二次型的秩,记为rankφ。当V的基底改变时,即
是对称矩阵,且称为二次型φ(x,x)在基底e1,e2,…,en之下的矩阵。A的秩rankA称为此二次型的秩,记为rankφ。当V的基底改变时,即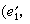
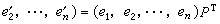 ,二次型φ(x,x)在新基底e姈,e娦,…,eń之下的矩阵变成B=PAP T,仍为对称矩阵,且与A是合同的。所以,研究二次型的合同性可归结为研究对称矩阵的合同性。
,二次型φ(x,x)在新基底e姈,e娦,…,eń之下的矩阵变成B=PAP T,仍为对称矩阵,且与A是合同的。所以,研究二次型的合同性可归结为研究对称矩阵的合同性。
V上的二次型也可看成F上的变元x1,x2,…,xn的二次齐次函数,又称为n元二次齐式或n元二次型,它与对称矩阵和对称双线性型都是一一对应的。当F为实数域R时,可以证明必有V的一组基底使二次型φ(x,x)有如下的形式
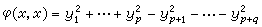 , (3)
, (3)
式中p+q=rankA。(3)称为实二次型φ(x,x)的实标准形。若(3)中的系数不限于±1,则(3)又可化为 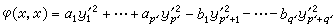 ,(4)并称为实二次型φ(x,x)的实对角型。式中αj、bk均大于零。所谓惯性定理,即实二次型φ(x,x)中的p、q、p┡、q┡必满足p=p┡,q=q┡,亦即(3)中的p、q或(4)中的p┡、q┡是由φ(x,x)惟一决定的合同不变量,分别称之为φ(x,x)的正、负惯性指标,而s=p-q称为φ(x,x)的符号差。易知,rankφ、s、p、q四个数都是合同不变量,其中任意两个都可惟一决定标准形(3)。
,(4)并称为实二次型φ(x,x)的实对角型。式中αj、bk均大于零。所谓惯性定理,即实二次型φ(x,x)中的p、q、p┡、q┡必满足p=p┡,q=q┡,亦即(3)中的p、q或(4)中的p┡、q┡是由φ(x,x)惟一决定的合同不变量,分别称之为φ(x,x)的正、负惯性指标,而s=p-q称为φ(x,x)的符号差。易知,rankφ、s、p、q四个数都是合同不变量,其中任意两个都可惟一决定标准形(3)。
当 F为复数域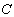 时,作为实二次型的推广有所谓埃尔米特二次型。若
时,作为实二次型的推广有所谓埃尔米特二次型。若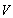 为
为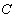 上的线性空间,从
上的线性空间,从 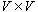 到
到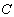 的映射φ满足
的映射φ满足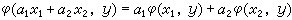 ,
,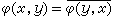 ,式中x,y在
,式中x,y在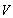 中,α1、α2在C 中,则φ称为
中,α1、α2在C 中,则φ称为 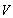 上的埃尔米特双线性型。由此可推出
上的埃尔米特双线性型。由此可推出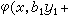
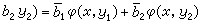 ,式中x、yj在V中,
,式中x、yj在V中,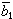 、
、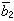 是b1、b2的共轭复数,均在
是b1、b2的共轭复数,均在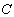 中。此时φ(x,x)称为埃尔米特二次型。易知,φ(x,x)∈R。若{e1,e2,…,en}是V 的基底,
中。此时φ(x,x)称为埃尔米特二次型。易知,φ(x,x)∈R。若{e1,e2,…,en}是V 的基底,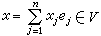 ,则
,则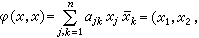
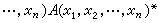 ,式中
,式中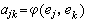 ,
,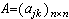 ,且
,且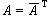 。因此,当
。因此,当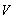 的基底取定时,埃尔米特二次型φ(x,x) 则由一个埃尔米特矩阵惟一确定。实二次型的基本性质都可推广到埃尔米特二次型上。例如,将(3)、(4)中的y嵃、y
的基底取定时,埃尔米特二次型φ(x,x) 则由一个埃尔米特矩阵惟一确定。实二次型的基本性质都可推广到埃尔米特二次型上。例如,将(3)、(4)中的y嵃、y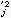 分别换为
分别换为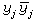 、
、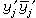 ,就得其标准形与对角型;也可定义其正或负惯性指标、符号差,建立其惯性定理。
,就得其标准形与对角型;也可定义其正或负惯性指标、符号差,建立其惯性定理。
所谓正定(恒正)的埃尔米特二次型或正定的实二次型φ(x,x)是指对于V的非零向量x,有φ(x,x)>0。可以证明,对于φ(x,x),下述的命题是等价的:
(1)φ(x,x)是正定的。
(2)A是正定矩阵。
(3)有非奇异矩阵Q使A=Q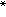 Q,式中Q
Q,式中Q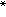 表Q的共轭转置矩阵。
表Q的共轭转置矩阵。
(4)有对角元全为正的上三角矩阵M,使A=M*M,式中M*表M的共轭转置矩阵。
(5)A的所有主子式全为正。
(6)A的j阶主子式之和全为正,j=1,2,…,n,这里n=dimV。
(7)A的所有左上角主子式(顺序主子式)全为正。
(8)A 的所有特征值全为正。
(9)φ(x,x)的正项指标p =n,这里n=dimV。
若将上述正定定义中的“>”,分别换为"≥"、“<”和“≤”,即得出φ(x,x)关于半正定、负定和半负定的定义。这些定义之外的其他情形,称为不定型。若将上述的⑤、⑥、⑧中的“正”改为“非负”,则得半正定的充分必要条件。φ负定即-φ正定,φ半负定即-φ半正定,由此可得出负定、半负定的某些充分必要条件。
埃尔米特二次型与实二次型分别在酉变换与正交变换下的性质,无论是在理论上还是在实用上都具有重要的意义。在酉变换(正交变换)下,化埃尔米特二次型(实二次型)为标准形时,可先在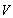 的任一基底下找出埃尔米特二次型对应的埃尔米特矩阵A,再求出A的全部特征值,即得φ(x,x)的标准形
的任一基底下找出埃尔米特二次型对应的埃尔米特矩阵A,再求出A的全部特征值,即得φ(x,x)的标准形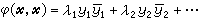
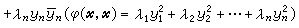 ,式中的(y1,y2,…,yn)是x在V某一基底下的坐标;λ1,λ2,…,λn是φ(x,x)在V的任意基底下的对应矩阵A的全体特征值。埃尔米特矩阵必有n个线性无关的特征向量。令以λ1,λ2,…,λn为对角元的对角矩阵
,式中的(y1,y2,…,yn)是x在V某一基底下的坐标;λ1,λ2,…,λn是φ(x,x)在V的任意基底下的对应矩阵A的全体特征值。埃尔米特矩阵必有n个线性无关的特征向量。令以λ1,λ2,…,λn为对角元的对角矩阵 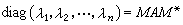 ,则M的列向量依次为各λj对应的A的特征向量,将这些向量正交化,即得所求的酉矩阵。实二次型为埃尔米特型的特例,所以也可用此方法求出实二次型的正交矩阵。
,则M的列向量依次为各λj对应的A的特征向量,将这些向量正交化,即得所求的酉矩阵。实二次型为埃尔米特型的特例,所以也可用此方法求出实二次型的正交矩阵。
二次型的理论在物理学、几何学、概率论等学科中都已得到了广泛的应用。在二次型的研究中已由域上二次型的算术理论发展到环上二次型的算术理论,它们与代数数论、数的几何等都有密切的联系。此外,在多重线性代数中使用二次型还可定义比外代数更广的克利福特代数。