[拼音]:tiaohe hanshu
[外文]:harmonic function
在某区域中满足拉普拉斯方程的函数。通常对函数本身还附加一些光滑性条件,例如有连续的一阶和二阶偏导数。当自变量为n个(从而区域是n维的)时,则称它为n维调和函数。例如,n=2时,调和函数u(x,y)在某平面区域内满足方程
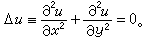
若所考虑的区域包含一个闭圆域,例如x2+y2≤R2,则有下列关于调和函数的平均值公式:
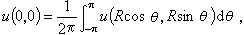
即u(x,y)在圆心的值等于圆周上的积分平均值。
更一般地,圆内任何一点x=rcosφ,y=rsinφ(0≤r<R)处调和函数 u=u(r, φ)的值可以由下列泊松公式给出:
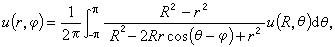
形如上式右端的积分称作泊松积分。
设u(x,y)为平面区域G中的调和函数,且在G的闭包上连续,则借助于平均值公式可以证明,它不能在G 的内部取其最大值与最小值,除非它恒等于一常数。这就是调和函数的最大、最小值原理。
由泊松积分出发可解决下列狄利克雷问题:在区域G的边界嬠G上给定一连续函数 ƒ(x,y),要求给出G中的调和函数u(x,y),使其在嬠G上取ƒ(x,y)的值,即
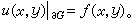
在G的边界嬠G满足一定的条件下,这个问题的解存在且惟一。
对于高维的调和函数,也有与上述类似的最大、最小值原理,平均值公式以及相应的狄利克雷问题解的存在和惟一性定理。
二维调和函数与解析函数论有着密切联系。在某区域内的调和函数一定是该区域内某解析函数(可能多值)的实部或虚部;反之,某区域内的解析函数其实部与虚部都是该区域内的调和函数,并称其虚部为实部的共轭调和函数。用复数z=x+iy的记法,将u(x,y)写成u(z),若u(z)在│z│<R内调和,在│z│≤R上连续,则泊松公式就成为
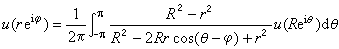
(0≤r<R)。
对于任何α,│α│<R,此式还可写成
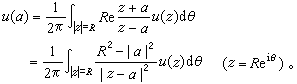
泊松积分是近代复变函数论中一个重要的研究工具,由此出发,可得出函数论中一系列重要结果。
若u(x,y)满足“重调和”方程
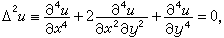
则称u是重调和函数,它是数学物理方程理论中的一个重要函数类。调和函数和重调和函数,在力学和物理学中都有重要的应用。类似地也有高维的重调和函数。
由于拉普拉斯方程是椭圆型方程的一个特殊情况,故后者的解的一般性质也是调和函数的性质。