[拼音]：zhengjiaoxi
[外文]：orthogonal system
互相正交的函数系的简称。平面上两个向量α＝(α1，α2)和b=(b1，b2)的正交性可用内积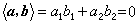
刻画。对［α，b)］上平方可积函数ƒ（x）和g(x)，可用
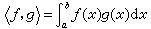定义内积，而且用〈ƒ，g〉=0定义正交性。在这个定义下，上面许多几何事实可以移植到该函数空间。由此便产生了正交系的概念：设
都异于零且两两正交，则称{φk(x)}是[α，b]上的正交函数系。又，若
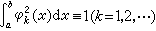，则称正交系{φk(x)}是就范的。正交系在分析学中有着重要地位。在许多数学分支，例如，微分方程、积分方程、计算方法、实函数、复函数与泛函分析中常会遇到它们。
最早出现且也是最重要的正交系是［-π，π］上就范正交的三角函数系：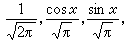
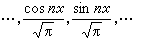。它的出现与弦振动问题有着密切联系。对它的深入研究曾对整个分析学的发展起过很大的促进作用。除三角函数系外，正交多项式系、哈尔系、拉德马赫尔系和沃尔什系也是有较大理论和应用价值的正交系。哈尔系、拉德马赫尔系和沃尔什系都是 [0，1]上就范正交系。
哈尔系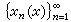
是由匈牙利数学家 A.哈尔于1910年提出的，定义如下：
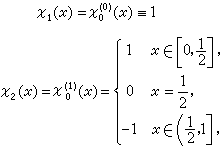
若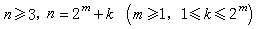
，那么
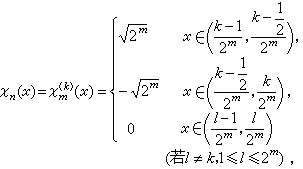
在间断点上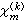
(x)等于左、右极限的算术平均。
拉德马赫尔系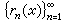
是德国数学家H.拉德马赫尔于1922年提出的，定义如下：
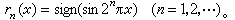
沃尔什系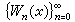
是由美国数学家J.L.沃尔什于1923年提出的，定义如下：
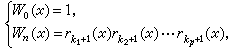
（当 n≥1且其二进表示为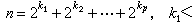
）。
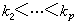平面上任意两个正交的单位向量{ e1，e2} 都是一组基，即任一平面向量α可表示为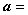
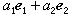的形式。[α，b]上平方可积函数空间L2[α，b]中的函数是否也可用正交系作类似的表示呢？回答是有时可以，有时不可以。 这取决于正交系的完备性。 设{φn(x)}是［α，b)］上就范正交系，
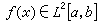，称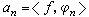
为ƒ(x) 关于正交系{φn(x)}的傅里叶系数。假如
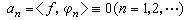仅当 ƒ(x)呏0时才成立，则称 {φn(x)}是完备的。前面所说的三角函数系、哈尔系、沃尔什系都是完备的，拉德马赫尔系不是完备的。若{φn(x)}是完备的就范正交系，那么对于一切ƒ(x)∈L2[α，b]有展开式
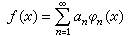。此式的含义是其部分和序列
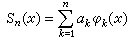在L2[α，b)]中收敛于ƒ(x)。反之，若上式对一切ƒ(x)∈L2[α，b]成立，则{φn(x)}必须是完备的。
一般地，设 H是希尔伯特空间，则当内积〈x，y〉=0时，称元素x和y是正交的。正交系是指异于零且相互正交的元素系。同样可以定义就范、傅里叶系数和完备性等概念。当正交系最多只有可列个元素时，可以证明，就范正交系{xn}的完备性是一切元素y∈H有展开式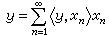
的充要条件。通常称此展开式为按{xn}的正交展开或傅里叶展开。