[拼音]：fanhan fenxi
[外文]：functional analysis
研究拓扑线性空间到拓扑线性空间之间满足各种拓扑和代数条件的映射的分支学科。它是20世纪30年代形成的。从变分法、微分方程、积分方程、函数论以及量子物理等的研究中发展起来的，它运用几何学、代数学的观点和方法研究分析学的课题，可看作无限维的分析学。半个多世纪来，一方面它不断以其他众多学科所提供的素材来提取自己研究的对象和某些研究手段，并形成了自己的许多重要分支，例如算子谱理论、巴拿赫代数、拓扑线性空间（也称拓扑向量空间）理论、广义函数论等等；另一方面，它也强有力地推动着其他不少分析学科的发展。它在微分方程、概率论、函数论、连续介质力学、量子物理、计算数学、控制论、最优化理论等学科中都有重要的应用，还是建立群上调和分析理论的基本工具，也是研究无限个自由度物理系统的重要而自然的工具之一。今天，它的观点和方法已经渗入到不少工程技术性的学科之中，已成为近代分析的基础之一。
泛函分析的起源
泛函分析的源头之一是变分法。18世纪形成的变分法的核心课题是研究形如
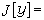
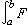
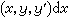
（或更复杂）的积分的极值。这里函数 y＝y(x)是在某个集合Y上变动，例如Y可以是［α，b］上具有连续导函数(或再附加一定的约束条件，如y(α)＝0，y(b)＝1等)的函数的全体。如果说微积分是研究以数 x为自变元的函数ƒ(x)，那么变分法就是研究以函数y为自变元的函数J[y]。函数y 在这里被视为“点”。19世纪末，J.（-S.）阿达马首先给这种函数的函数J[y]冠以“泛函”的名称。在泛函J[y]的极值的研究中，需要考察与一个函数y0相“邻近”的一切函数，这就向人们暗示:Y 中的函数(“点”)与函数(“点”)之间有着某种衡量远近的几何度量，从而Y是具有某种度量的、由函数(“点”)构成的“空间”。但是，认识到要把函数视为点，把某些函数构成的集合视为空间（函数空间），还是在和其他学科长期发展的历史过程中形成的。所以就连“泛函”一词的出现也并不是在变分法形成的18世纪，而是直到19世纪末。
泛函分析的另一个源头是积分方程。自从1823年N.H.阿贝尔从力学问题中提出并研究积分方程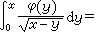
ƒ(x)以后，19世纪末在微分方程，例如在狄利克雷等问题的研究中，出现了上述积分方程的推广形式，所谓沃尔泰拉型积分方程。（E.）I.弗雷德霍姆1900年又对积分方程
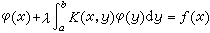作了重要研究。后者引起了D.希尔伯特的极大兴趣。1904～1906年，希尔伯特在这方面完成了 6篇论文。他在实连续积分核K(x，y)是对称的(即K(x，y)=K(y，x))的条件下，获得许多比弗雷德霍姆更深入的结果。例如，证明特征值是实的，给出预解式的形式与特征展开等等，这些通常称为希尔伯特谱论。希尔伯特利用正交展开将积分方程求解问题化成无限阶的线性方程组求解问题，并在此基础上引入无限维（实）欧几里得空间l2，即满足
的实数列α＝(α1，α2，…，αn，…)全体。他提出了l2上有界双线性形式、有界线性形式(即所谓连续线性泛函)以及两种收敛（即所谓的强、弱收敛）等概念，给出了l2上的选择原理(即所谓的闭单位球的弱紧性)，还发现连续谱的存在等等。这表明用代数方法来研究分析中某些课题是很自然的。
泛函分析的形成
泛函分析作为学科的形成，以致它的整个发展，至今主要是围绕着对偶理论和算子谱论展开的。
度量空间和函数希尔伯特空间几乎与希尔伯特同时，M.R.弗雷歇就提出并研究了以具体函数类为主要背景的抽象度量空间（也称距离空间）以及度量空间中的紧性、完备性、可分性等泛函分析的基本概念。这里包含着一般拓扑学（又称点集拓扑学）的萌芽。另一方面，希尔伯特的学生E.施密特在积分方程的研究中发展了希尔伯特谱论。他在1908年的论文中已使用复l2、内积和范数的符号，给出了正交、闭集、向量子空间的定义，并证明在闭向量子空间上投影的存在性。这是基本的几何概念正式进入了泛函分析。1902年H.L.勒贝格的积分理论问世(似乎当时希尔伯特不知道)，有力地加速泛函分析的形成。1906～1907年，E.菲舍尔和F.（F.）里斯利用新积分工具相互独立地证明了里斯—菲舍尔定理。里斯在此基础上引入平方可积函数空间L2[α，b]，证明了它的完备性、可分性，并很自然地将弗雷德霍姆理论推广到K(x，y)是矩形[α，b]×[α，b]上平方可积函数的情形。
连续线性泛函泛函分析的一个基本概念。围绕对它的研究形成的对偶理论至今仍是泛函分析中心课题之一。对它的研究最早可追溯到C.博莱特(1897)提出要用连续性条件来刻画一定函数类上的连续线性映射T:E→F。1903年阿达马在E是C[α，b]([α，b]上连续函数的全体)，F是实数域，当{ƒn}一致收敛于ƒ 时，Tƒn→Tƒ的情况下，将T 表示成一列积分的极限的形式。但这种表示不惟一，并且有极大任意性。后来在实l2空间上，弗雷歇和里斯独立地在T 是所谓强连续假设下给出简单而惟一的表示，即希尔伯特空间l2上的连续线性泛函表示定理。里斯在1909～1910年又相继给出C[α，b]、Lp[α，b]、lp(p>1)上的表示定理。在这些表示定理的证明中实质上已蕴含线性子空间（又称向量子空间）上连续线性泛函必可延拓到全空间的事实。E.黑利从1912年开始（中间经过第一次世界大战的中断），直到1921年用“赋范数列空间”(他并未用这个名称)代替具体的C[α，b]、Lp[α，b]、lp等而考虑较抽象形态的延拓问题。他使用了凸性以及在有限维空间情况下早为H.闵科夫斯基用过的术语，如支撑超平面等。
巴拿赫空间在许多具体的无限维空间以及它们上面相应的收敛性出现之后，抽象形态的线性空间（向量空间）以及按范数收敛的出现就成为自然的了。1922～1923年，E.哈恩和巴拿赫（同时还有N.维纳）独立地引入赋范线性空间。当时的讨论事实上都限于完备的赋范线性空间。1922年哈恩从当时分析数学许多分支已达到的成果和方法中提炼出了共鸣定理。1927年H.施坦豪斯和巴拿赫用完备度量空间的第二纲性代替原来所谓“滑动峰”证明方法，给出现今常见的证明。1922～1923年巴拿赫又得到了压缩映射的不动点定理、开映射定理。1927年哈恩完全解决了完备赋范线性空间上泛函延拓定理的证明，并第一次引入赋范线性空间E的对偶空间（共轭空间）K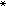
（当时称为极空间）。两年后，巴拿赫用同样方法也得到同样结果（后来，他承认哈恩的优先权），并看到这个定理可以推广。这个推广形式在后来的局部凸拓扑线性空间理论中起了重要作用。1931年巴拿赫将他1923～1929年的工作以及当时主要成果写成《线性算子理论》一书，书中大部分讨论他1929年开始研究的弱收敛，这又成为局部凸拓扑线性空间理论出现的先导。在同一书中还发表了完备赋范线性空间上连续线性算子值域不是第一纲集便是全空间以及闭图像定理等重要结果。这时，作为完备赋范线性空间理论的独立体系已基本形成，它的许多结果已成为泛函分析应用中的强有力工具。人们为纪念他的功绩，把完备赋范线性空间称为巴拿赫空间。近年来，人们特别感兴趣的一个领域是研究巴拿赫空间的几何学。
事实上，希尔伯特谱论已是泛函分析算子谱论的开始（虽就算子而言是具体的由核K(x，y)所确定的积分算子，可就观念和研究方法而言却是代数的）。
然而早在18世纪，人们已从数学的各个领域的经验中开始对算子有所意识，特别从种种方程的解具有叠加性中了解到许多重要运算，例如微分运算、积分运算等都具有线性。但作为谱论的直接源头是弗雷德霍姆理论，这个理论与有限阶线性方程组求解理论极其相似。人们自然会问：怎样的线性运算和熟知的有限维空间上线性变换的若尔当型与弗雷德霍姆理论有相似的性质？这个问题在里斯之前，有人探索过，但未解决。1916～1918年，里斯给出了完全的回答。他先限于lp，后又考察C[α，b]，他未用希尔伯特的双线性形式，而直接用术语算子代替它，引入全连续算子概念。最终他又把讨论基本上推广到了巴拿赫空间上。其中涉及共轭算子的某些结果，后由J.P.绍德尔(1932)补充完成。通常称它为里斯—绍德尔理论。里斯受希尔伯特发现连续谱现象的启发，用与希尔伯特完全不同的但具有典型泛函分析意味的方法得到l2上有界自共轭算子A的谱分解: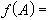
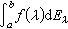，其中ƒ是[α，b]上的连续函数，{Eλ}是l2上一族投影算子。这对希尔伯特发现的连续谱或说应是近似点谱做出了很好的解释。或说：非特征值的连续谱所相应的是广义特征向量。当然他当时的表达形式是较原始的。20世纪20年代是量子力学的大发展时期，不断出现的新思想要求寻找合适的数学工具。物理学家们最终发现，可观察量的性质与希尔伯特空间（当时还没有这个名称）上自共轭算子的性质具有不平常的一致性，而希尔伯特所提出的数学上的谱可以用来解释物理学上原子的谱，因此纷纷来找希尔伯特帮助。1926年，作为助手来到希尔伯特身边的J.冯·诺伊曼开始曾以 L2[α，b]上积分算子进行尝试，发现物理学家所必须运用的狄喇克 δ－函数的概念中，从当时的数学看来，包含着矛盾。冯·诺伊曼为提供量子力学的严格数学基础，于1929～1932年，正式引入并定名抽象的（即现在的）希尔伯特空间概念。鉴于物理学上的可观察量以及奇异积分方程、微分方程中出现的重要算子都是无界的，冯·诺伊曼引入稠定闭算子概念。他做出系统的奠基性的工作：给出了无界自共轭算子的谱分解，发现对称算子和自共轭算子的区别，建立了对称算子亏指数理论，又给出了酉算子和正常算子谱分解，证明了量子力学中交换关系的表示在酉等价意义下是惟一的（即量子力学体系的数学描述本质上只有一种）等等。此后作为单个算子谱论，人们最主要兴趣是非正常算子谱论和巴拿赫空间算子谱论。巴拿赫的《线性算子理论》一书问世以及冯·诺伊曼的谱理论的出现，标志着泛函分析已作为独立的数学分科诞生。在形成过程中，它的每个重要结果都伴随着它在其他领域中的许多有价值的应用。
泛函分析的重要分支
巴拿赫代数20世纪30年代初代数环论的重要进展以及它在群表示论上的应用，促使冯·诺伊曼于1935年开始以很大的兴趣研究了希尔伯特空间 H上有界线性算子全体B(H)的(对称)弱闭子环，获得（部分与F.J.默里合作）完整而深入的结果。后人称这种算子环为冯·诺伊曼代数，也称W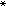 
代数。1941年又出现了И.М.盖尔范德在巴拿赫代数方面的开创性工作，将算子谱推广到巴拿赫代数中的元素。特别是他(部分与М.A.奈玛克等合作)完成系统而精美的C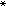代数（虽是特殊的，但重要的巴拿赫代数）理论。代数的方法在这里充分显示了威力。这些代数理论汇成了泛函分析的新分支─巴拿赫代数（包括W 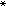代数）。它不仅成为建立局部紧群上调和分析以及后来50年代研究局部紧群的线性表示理论的重要工具，而且在研究经典分析某些课题中也取得了令人惊异的效果。
泛函分析的另一重要分支是拓扑线性空间理论。在弗雷歇引入距离，并用它来统一过去分析学中的许多重要收敛时，就知道 [α，b]上一列函数的“点点收敛”概念是不能用距离收敛来描述的。跨入30年代，泛函分析中大量使用弱收敛、弱拓扑。它们都不能用距离来描述，这就很自然地要把赋范线性空间理论发展成更一般的拓扑线性空间理论，其中最主要的成就是局部凸拓扑线性空间理论。这一分支的发展是与一般拓扑学的发展紧密联系在一起的。拓扑学方法在这里发挥了极重要的作用。勒雷—绍德尔不动点定理是有力的例证之一。从1935年开始，经过十多年时间，这一分支终于形成，它的许多重要结果不仅在泛函分析中有广泛的应用，也为其他分析学科的深入研究提供了基本框架和有力的工具。
广义函数论泛函分析中具有广泛应用的又一重要分支。30年代开始，很多数学家研究微分方程的“弱解”，这自然地导致广义导(函)数概念。应注意的是点点不连续的函数可能有广义导数而仅在一点不连续的函数却可能没有广义导数。对一个具体的微分方程，所需的广义导数可以容纳在当时已形成的巴拿赫空间理论的框架之中。然而对物理学家P.A.M.狄喇克引入的“不存在的”函数δ，通过如下一些操作，例如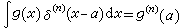
(这里g是n次连续可微函数)，
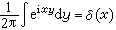等等，竟能得到正确的结论，这在那时候是使数学家们费解的。С.Л.索伯列夫(1936)迈出了决定性的一步，他除了引入了广义导数（后人称为索伯列夫导数），更重要的是将δ(n)(x-α)视为开集Ω上无限次可微且具紧支集的函数空间D(Ω)上的线性泛函，即
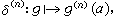这在数学上是完全可以接受的。他用这种方式处理δ、δn，在双曲型方程的柯西问题中取得了重要成功。但他对这种“函数”所规定的连续性概念尚不能容纳在当时形成的巴拿赫空间理论中。随着拓扑线性空间理论以及调和分析理论的发展，终于在1945年出现了L.施瓦尔茨的分布论(又称广义函数论)，完全解决了广义函数（包括δ－函数）的傅里叶变换问题，并将这方面已有的种种重要观念汇成了统一和完整的理论。广义函数论把函数概念提高到一个新阶段，它一出现就强有力地推动偏微分方程的发展。例如，50年代末出现L.赫尔曼德尔的叶理论，紧接着60年代又出现了伪微分算子理论和傅里叶算子理论。从此，偏微分方程的研究出现了新局面。
上面所谈到的一些重要的成果和分支，除其中个别定理（如不动点定理）外，都属于泛函分析中的线性部分。就泛函分析的起源而言，变分法中所讨论的泛函J[y]就已经是非线性的了。然而就发展的现状来说，泛函分析中非线性理论远没有达到线性理论部分那样丰富多采的结果。这很可能是由于线性与非线性问题有本质区别，而线性问题要比非线性问题简单得多。对分析学各个领域中出现的各种形式的问题，只要本质上属于线性的问题，尽管是很复杂的问题，相对的说，人们是易于取得成功的。在丰富成果的基础上自然容易形成统一而漂亮的线性理论，获得广泛的应用。然而，现实中非线性问题远比线性问题多。由于处理上的困难，不少非线性问题就用线性的近似来代替。随着认识的深入，线性问题研究到一定阶段，人们自然就向非线性问题进军，这就为泛函分析非线性部分的发展提供了前提。围绕着非线性积分方程、非线性积分微分方程以及各种近似求解法等等，已逐渐形成了在应用上具有一定广泛性的泛函分析的非线性理论，例如近似解理论、单调算子理论、隐函数理论、拓扑度理论、分歧理论等等（见非线性算子、大范围变分法）。随着近代微分几何、拓扑学和大范围分析的发展，今后非线性泛函分析定将有更广阔的前景。