物体的振动

浏览

[拼音]：wuti de zhendong

[外文]：vibration of bodies

物体围绕一平衡位置的往返重复运动。物体的一部分或整体受力的作用产生形变，形变部分具有恢复其原来状态的力(恢复力，或称具有形变势能)。例如固体的弹性力和液体的表面张力等都可成为恢复力，此外还可以有外加的恢复力，例如把弦或膜拉紧的张力等。在外加作用力消失后，恢复力使变形的物体向平衡位置运动，形变势能逐渐转化为动能，在物体达到平衡位置时，形变势能为零而动能最大；由于惯性作用，物体继续沿与原形变方向相反的方向偏离平衡位置，产生新的形变，动能逐渐转化为形变势能，在动能为零时形变势能最大，偏离平衡位置的距离也最大。如此重复，形成物体的振动。

实际常见的物体振动可以理想化地分为弦、棒、膜、板和壳的振动。

弦的横振动

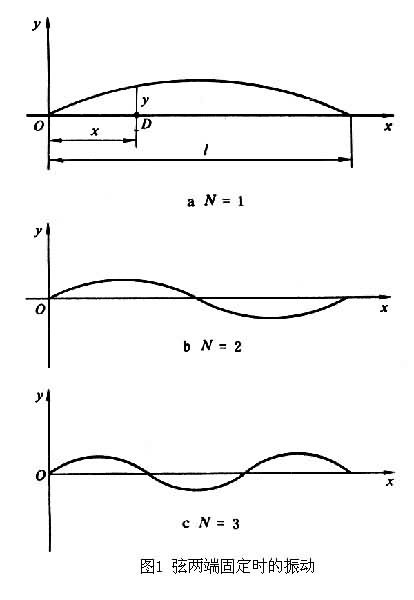
把一根长度为 Л的柔软（无刚性）且尺度和质量完全均匀的弦拉紧并两端固定（图1a），用手指轻弹弦即可激起弦的横振动。它的振动方程为

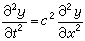， (1)

式中y为弦上坐标为x的一点D在横方向的位移，单位为米(m)，t是时间，单位为秒(s)，с是波动在弦上传播的速度，单位为米每秒(m/s)

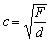， (2)

F是弦上的张力，单位为牛[顿](N)，d是弦的线密度，单位为千克每米(kg/m)。弦自由振动时的频率为

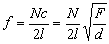， (3)

式中N＝1，2，3，…。N＝1时频率最低，称为基频，对应的振动方式称为一次谐波；N＝2时称为二次谐波（图1b），依次类推。可见二次以上的高次谐波的频率是基频的整数倍。在稳定振动的情况下，弦中的波是驻波（见波），因此 N次谐波除两端固定无位移外，弦上还有N-1个无位移的点（图1b、图1c），称之为节点。而位移最大的部分称为波腹。根据式(3)可知，改变弦的长度Л或张力F或线密度d，都可以改变弦振动的频率。弦乐器如胡琴、琵琶和提琴等，都是根据弦的这个振动原理制成的。

图1

膜的振动

一个柔软无刚性的薄膜，厚度及质量完全均匀，如果它周边用力向外拉紧并固定，即形成一个可以振动的膜。常见的膜周边的形状是矩形和圆形。考虑如图2中所示的矩形膜。若膜平面为xy平面，м是膜上坐标为(x，y)的一个点，膜振动时м点离开它静止时位置的位移为z，于是可得膜的振动方程为

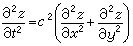， (4)

式中

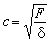(5)

是波动在膜中传播的速度，F是膜边缘上每单位长度上的张力，单位为牛顿每米(N/m)，δ是膜的面密度，单位为千克每平方米(kg／m2)，t是时间。式(4)表明膜是二维的“弦”。膜的振动频率为

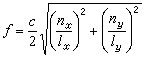， (6)

式中nx、ny＝1，2，3，…，Лx和Лy是矩形膜的边长。当nx＝ny＝1时，膜的振动频率最低，是基频(图3a)。当nx＝1，ny＝2时，膜的振动方式如图3b所示，除周边外还有一个纵向的节线(其上诸点的位移为零)，节线把膜分成左右两部分，在振动时两部分的相位相反，即在一边向上运动时另一边向下运动。当nx＝1，ny＝2时，膜被一横节线分成相位相反的两部分(图3c)。只有当nx＝ny＝2，3，4，…时，膜的振动频率是基频的整数倍，即高次谐波。而nx≠ny时，振动频率是基频的泛音。

图2 图3

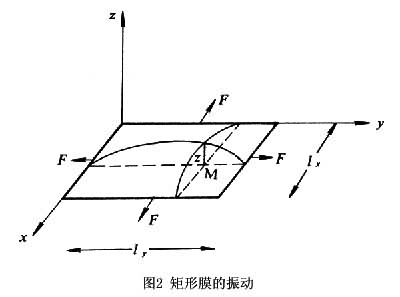
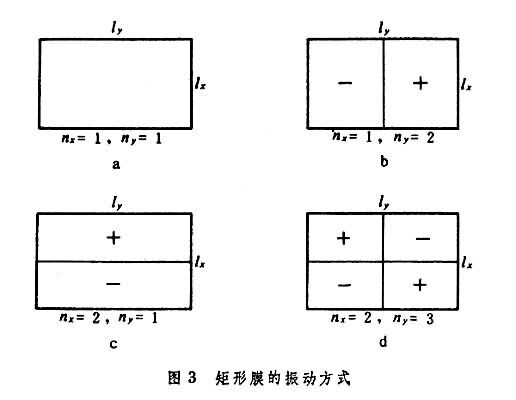
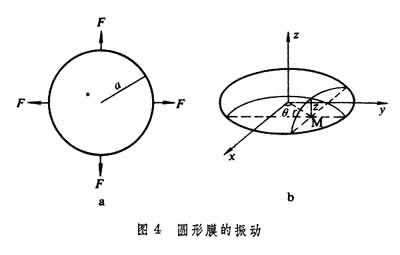
图4所示是半径为a的圆形膜，用柱坐标表示它的振动方程为

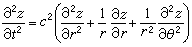。 (7)

(r，θ)为膜上м点的极坐标，z为м点的位移。圆形膜自由振动时的频率为

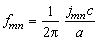， (8)

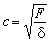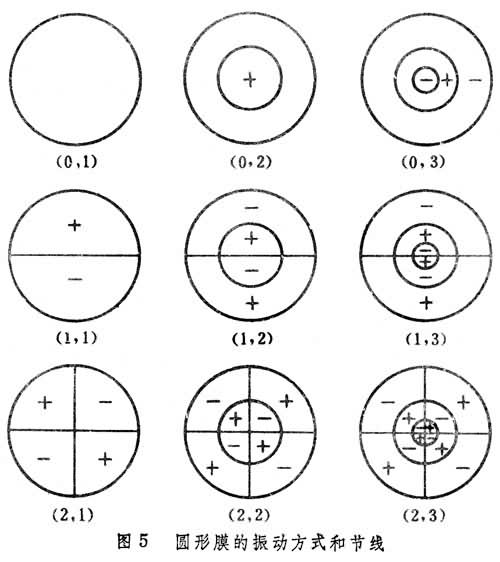
其中，jmn是无量纲的常数，随不同的m、n而异。表中给出几种振动方式的频率，而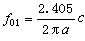，是圆膜振动时的基频。其他频率都不是基频的整数倍，是它的泛音。圆膜振动时的振动方式及节线如图5所示。

图4 表 图5

棒的振动

横截面尺度小于长度的固体称为棒或梁。棒受作用力的扰动后可以产生振动，称为棒的振动。其形式因受力方式而异，一般有纵振动、弯曲振动和扭转振动三种。棒或梁的刚性可以支撑它本身的重量，故不像弦那样必须在两端固定拉紧才能振动，只需把棒架起即可使棒产生振动。

棒的纵振动

对各向同性密度均匀的材料制成的细棒，用锤沿棒轴方向轻击一端表面的中心，如图6所示，即可激起棒的纵振动，振动时棒中质点的运动方向与棒轴平行。棒的振动方程是

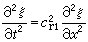， (9)

式中ξ 是距A 端x 处棒截面的位移。根据棒两端的情况，棒可以有不同的振动形式。一般有三种，即棒两端全是自由的、两端全是固定的和一端自由一端固定三种情况。两端都是自由的棒振动频率为

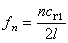， (10)

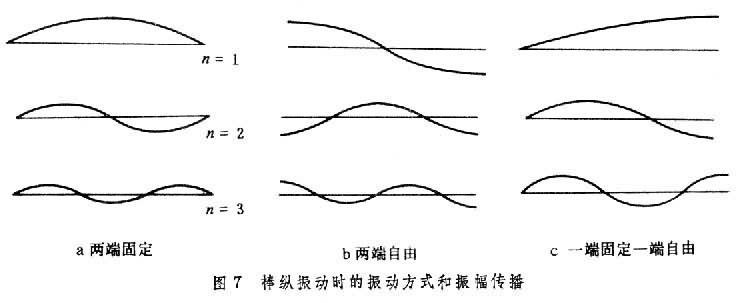
式中Л是棒长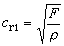，，是细棒中纵波传播速度，n＝1，2，3，…。其振动方式如图7b所示，纵坐标表示振动时棒各部分的位移。图中也给出节点的位置。图7a是两端固定的棒的振动方式，从图可看出其振动频率与两端自由的棒振动频率相同，只是节点的位置不同。一端固定一端自由的棒纵振动时的频率为

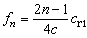。 (11)

与式(10)相比，可知一端固定另一端自由的棒，作纵振动时的基频只为两端自由或两端固定时的频率的一半，而且只有奇次谐波。

图6 图7 棒的弯曲振动

沿与棒垂直的方向击棒，可激起棒的弯曲振动，振动时的形状如图8所示。棒做弯曲振动时的振动方程是

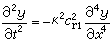， (12)

式中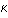是棒横截面的回转半径。与棒纵振动的情形类似，其振动频率也与棒两端的边界条件有关。一般端点条件有两种情况：即棒的一端自由，另一端固定；棒两端都是自由的。根据两端的条件解式(12)，可得一端自由一端固定的棒做弯曲振动时的频率为

，

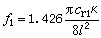f2=6.267f1，

f3=17.55f1，

……。两端自由的棒弯曲振动时的频率为

，

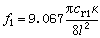f2＝2.756f1，

f3＝5.404f1，

……。

图8

在乐器中有些是利用棒的振动原理制成的，例如木琴、风琴的簧片、调音用的音叉等。

从以上所列频率看，棒做弯曲振动时，它的泛音都不是基频的整数倍。

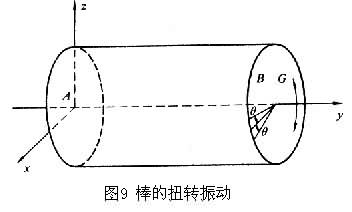
棒的扭转振动

棒除了能作纵振动和弯曲振动外，还可以作扭转振动，如图9所示。若截面为圆形的棒A 端的面与xz平面吻合并固定，棒轴与y轴吻合，在A端加一扭矩G，使A面上的半径转过一个θ角，然后撤去扭矩， 则AB棒即可做扭转振动。棒的每个截面都以y 轴为圆心往返转动。扭转振动的方程为

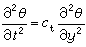， (13)

式中сt是无限固体中横波传播速度，θ是角位移。因A面固定，故无角位移，即节点。这与一端固定另一端自由的棒做纵振动时的频率相似，于是有

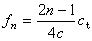。 (14)

图9

薄板的振动

适当增加膜的厚度可以形成薄板，薄板振动时的恢复力主要来自板的刚性，而不像膜是来自外加的张力。生活中常见的振动薄板多为圆形，如传声器或电话耳机中的薄金属片，乐器中的锣、钹、铙等。

均匀薄板对称振动时的振动方程是

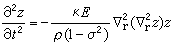， (15)

式中z是薄板与xy平面吻合时在z方向的位移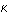，是面回转半径，对于厚度为τ的均匀薄板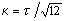，，E是板材的弹性模量，ρ是体密度，σ是泊松比(物体受力拉长时，横向单位长度收缩值与纵向单位长度拉长值之比)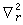，是用极坐标时拉普拉斯算符。圆形薄板振动时的频率与周边支撑情况有关，假设板做简谐振动，圆板周边在r＝a处固定，形成节线，则频率的表达式是

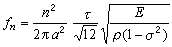。 (16)

用上式求得的基频及泛音频率为

，

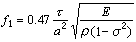f2＝3.88f1，

f3＝8.70f1，

……。

壳体的振动

将板弯曲成壳体，可以制成钟、磬、铃等发声的乐器。发声的壳多用金属制成，其振动频率与壳体的形状、尺寸、弹性和密度有关，除少数形状十分简单的壳体比较容易求出其振动频率外，对形状复杂的壳体，计算它的振动频率是比较繁难的。瑞利曾对长度大于直径并均匀的圆柱形壳体振动时的频率进行计算，算得的振动频率为

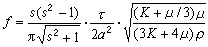， (17)

式中τ为壳体的厚度，K为体积模量，a为壳体的半径，s为壳体圆周对波长的倍数，即壳体圆周上的波节数为2s。

一般壳体乐器如钟磬等的横剖面均为圆形，但在中国出土文物中的古代编钟的横剖面却为椭圆形，而且表面上还有古书中称为“枚”的圆柱形乳突，用现代科学技术分析中国古代编钟的声学特性，结果表明椭圆形状及表面上的“枚”对钟的音质都有一定的作用。节线的位置及分布也符合科学原理。出土的编钟均完好无损，这一切都说明早在西周时代（公元前1066～前771），中国人已在乐器制造和合金冶炼方面有了相当高的工艺和技术水平。

参考书目
  1. L.E.Kinsler， et al.， Fundamentals of Acoustics， 3rd ed.，John Wiley & Sons， New York， 1982.
  2. R. W. B. Stephens and A. E. Bate，Acoustics and Vibrational Physics， 2nd ed.，Edward Arnold，London， 1966.
  3. 陈通、郑大瑞：古编钟的声学特性，《声学学报》，第3期，第161页，1980。
  4. J.W.S.Lord Rayleigh， Theory of Sound，Dover，NewYork， 1945.
阅读全文