[拼音]：xuanze gongli
[外文]：axiom of choice
公理集合论中的一条重要的公理，简记做AC。它可表述为：如果S是由不空的集合组成的一集合，则存在一个函数ƒ，使得对于S中的每一集合x，都有ƒ(x)∈x成立。换言之，当S是由某些不空集合组成的一集合，问是否存在一种原则（即函数ƒ），使得按照这一原则在S的每一集合x中都能恰好挑选出一个元素。在许多情况下，上述问题的答案是肯定的。但是在一般情况下，是否能肯定呢？当人们肯定回答时，它就称为选择公理。
19世纪，人们在数学论证中经常使用选择公理，但尚未深入研究它的不同的表现形式和推论。例如，1890年G.皮亚诺在证明常微分方程解的存在性定理时，陈述了选择公理，并且对它提出了怀疑。G.（F.P.）康托尔在研究序数理论时提出，是否每一集合都可良序的问题。1904年E.F.F.策梅洛证明了这一定理，即每一集合都是可以良序的。在证明中他用现代术语，严格地陈述了选择公理。G.康托尔最早使用选择公理的等价形式，即关于集合势的三分法原则:对于任意的集合S1与S2，下述三式
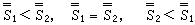
中恰有一个式子成立。其中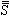
i表示集合Si的势。1915年F.霍尔托格斯证明了集合势的三分法原则与选择公理是等价的。自20世纪初以来，B.A.W.罗素、F.豪斯多夫、K.库拉托夫斯基等人先后发现和证明了，选择公理与乘积定理、良序定理、极大原理、佐恩引理等成百个数学命题是等价的，并且在数学的许多分支中有着广泛的应用。这就使选择公理更加引人注意了。比如，连续函数的ε-δ 型与序列型两种定义，由选择公理可以证明是等价的；但是没有选择公理，它们是不等价的。利用力迫方法可以证明，存在着选择公理不成立的模型，在其中有一函数ƒ和一个实数x0，使得ƒ于点x0在 ε-δ 型意义下是不连续的，在序列型的意义下是连续的即对于任意的序列
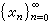，若
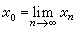则有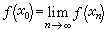
。又如，关于有穷集合的两种常见的定义：
（1）对于任意集合S，如果有一自然数n，使得S中恰有n个元素，则称S为有穷集合。S不是有穷集合时，就称为无穷集合。
（2）对于任一集合S，如果有S的一真子集合与S是一一对应的，则称S为D无穷的;当S不是D无穷时，就称S是D有穷的。在有选择公理时，①与②是等价的；在无选择公理时，它们是不等价的。利用力迫方法可以证明，存在着一个选择公理不成立的模型，在其中有一集合S，按照①它是无穷的，按照②它是D有穷的。
大量的事例说明选择公理是现代数学的一个基本原则和基本方法，没有它和它的等价形式，数学的许多分支将是寸步难行的。但是，选择公理是否合理和正确一直存在着争议。一些数学家怀疑、反对它，一些数学家毫无保留地赞同、应用它。各有各的理由。反对的理由之一是，按照它实数集合是可良序的，但至今人们没有找到它的良序。反对的理由之二是，1924年S.巴拿赫和A.塔尔斯基使用选择公理揭示了对球体的分解与组合的悖论（把一个球切成有穷个片断，然后再重新组合，可得到与原球有相同尺寸的两个球）。这样，选择公理就成了数学基础中的一个很突出的问题了。
60年代以来，J.迈切尔斯基等人提出一条相当基本的数学原理，称为决定性公理，并在此前提下证明了许多有趣的结果。例如：
（1）实数的不空集合的每一可数集族都有一选择函数；
（2）实数的每一集合都是勒贝格可测的。对于①选择公理是成立的；但对于②选择公理是不成立的。因为，使用选择公理就一定存在勒贝格不可测的集合。不难看出，上述①是选择公理的一种较弱的形式(对可数集合而言)，而②的否定式是选择公理的一种较强的形式。有这样一种可能，就是选择公理的一般形式不成立，而它的某些较弱的形式是成立的。P.贝尔奈斯、塔尔斯基、库拉托夫斯基、P.莱维、J.D.哈尔佩恩和T.J.杰希等人系统地研究了选择公理的较弱的形式，并且证明了它们可以由选择公理推导出来，但它们不能推导出选择公理；同时也揭示了这些较弱的形式在各自的应用中都是不可缺少的。选择公理有如下一些弱的形式。
（1）次序原则（简记做 OP）对于每一集合都是能够线序的。
（2）对于n个元素集合族的选择（简记做Cn）对于任一具有n个元素的集合族S(即若x∈S，则x恰有n个元素)，都有一函数ƒ，使得若x∈S，则ƒ(x)∈x。
（3）对于有穷集合族的选择（简记做ACF）对于任一有穷的集合族S（即若x∈S，则x为一有穷集合），都有一函数ƒ，使得若x∈S，则ƒ(x)∈x。
（4）序扩充原则（简记做 OEP）任一集合S的每一偏序都能够扩充到S的一线序（或称全序）。
（5）挑选原则（简记做SP）对于每一集合族S（它的任一元至少有两个元素）都存在一函数ƒ，使得对于S中任一元x，都有ƒ(x)≠═且ƒ(x)是x的一真子集合。
（6）ACW 对于任一良序集合，选择公理成立。
（7）素理想定理（简记做PIT）每一布尔代数都有一素理想。
上述①～⑦都是AC的推论。用A→B表示A蕴涵B，即在无选择公理的ZF中，有ZF├A→B。用A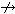
B表示A不蕴涵B，即ZF├A 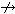B。已有下述结果：
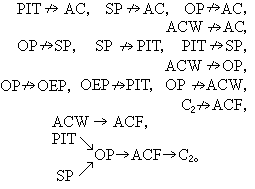
对于选择公理的研究说明，确立数学公理是十分严肃的科学研究工作，而绝不是能被少数数学家随心所欲的虚构。
- 参考书目
- H.Rubin and J.E.Rubin，Equivalents of the Axiom of Choice， North-Holland， Amsterdam， 1963.
- T.J.Tech，The Axiom of Choice， North-Holland Ams-terdam， 1973.