[拼音]:motai moxinglun
[外文]:modal model theory
模态逻辑的模型论。特别是指量词模态逻辑即一阶模态谓词逻辑的模型论。它从属于模态逻辑的三个主要研究方向,即公理学、语义学和代数学方向之一的语义学方向。模态逻辑的关系语义学(又称关系模型论)一般公认是由S.A.克里普克开创的。他于1959年发表在《符号逻辑杂志》上的题为《模态逻辑的一个完备性定理》一文中首先提出了关系模型(或称关系语义解释)的概念,并证明了带量词的S5(在该文中记为S5*)相对于该关系模型概念为完备的;稍后又接连发表几篇论文对各种正规和非正规模态系统提出了相应的关系语义解释,即关系模型概念。
如同许多重要的数学概念一样。关系语义学的提出也并非克里普克一人的功劳。在他的前后若干年,有近10位逻辑学家彼此独立地,正式或非正式地提出了相近的或略有不同的语义概念。其中值得一提的有S.坎格尔和K.J.J.欣蒂卡二人。欣蒂卡在1961年和1963年两度提出的”模型集合“与克里普克的关系语义解释有异曲同工之妙;而坎格尔则在1957年就正式提出了与克里普克的关系语义几乎完全一样的语义概念。只是所用术语不同而已。
设L为古典一阶语言(见模型论),作为非逻辑常项集合的L若在模态逻辑中考虑就成为一阶模态语言,此时不妨记作L◇(注意:L与L◇作为集合是完全一样的)。
所谓与语言L◇相应的模态结构U是指一个有序五元组〈W,A,凴,R,V〉。这里W 为一非空集合,其中元素称为“可能世界”。A为一非空集合,其元素称为“可能个体”。对于每个w ∈W,凴w为A的一个子集,R吇W×W为W上的二项关系,称为可达性关系。V(赋值)为定义在L◇上的函数,使得,对于L◇中的任一个体常量符号с,V(с)∈A,对于 L◇中的任一n元谓词符号F,n≥0,有V(F)吇W×An。
L◇中语句在W 的元素w 上的真定义象通常那样进行,所须注意的是:
第一,①w 喺с=d(式中с,d为L◇中的个体常量符号),当且仅当V(с)=V(d);
(2)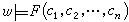 (式中F是L◇中的任一n元谓词符号,с1,с2,…,сn为L◇的n个个体常量符号),当且仅当<w,V(с1),…,V(сn)>∈V(F)。
(式中F是L◇中的任一n元谓词符号,с1,с2,…,сn为L◇的n个个体常量符号),当且仅当<w,V(с1),…,V(сn)>∈V(F)。
第二, 当且仅当w 喺φ(с)对L◇中的一切适合V(с)∈凴w 的个体常量符号с(假定每个可能个体均在L◇中有一个“名字”)。
当且仅当w 喺φ(с)对L◇中的一切适合V(с)∈凴w 的个体常量符号с(假定每个可能个体均在L◇中有一个“名字”)。
第三, 当且仅当存在某一可能世界υ∈W,适合〈w,υ〉∈R,使得v喺φ成立。
当且仅当存在某一可能世界υ∈W,适合〈w,υ〉∈R,使得v喺φ成立。
所谓语言L◇的一个模型 ,是指一有序偶
,是指一有序偶 上为真,记作
上为真,记作 喺φ。
喺φ。
需要区分各种类型的模型(或结构), (或U)称为T 模型(相应地,T 结构),如果R为一自反关系;称为S4模型(相应地,S4结构),如果R为一自反和传递关系;称为S5 模型(相应地,S5 结构),如果R=W×W,等等。
(或U)称为T 模型(相应地,T 结构),如果R为一自反关系;称为S4模型(相应地,S4结构),如果R为一自反和传递关系;称为S5 模型(相应地,S5 结构),如果R=W×W,等等。
一结构称为具有常论域的。如果对于任意 w ,υ∈W,均有凴w=凴v,也需要区分各种逻辑系统。量词逻辑系统 T、S4 和 S5等可以像G.E.休斯与M.J.克雷斯韦尔合著的《模态逻辑引论》(1972)书中所述的那样公理化,并且可以证明它们对于上面提到的相应的模型类为强完备的。设 l为一逻辑系统,那么lB就表示把公理模式 (通称巴坎公式)加入l 而得的新系统。此时,量词系统TB、S4B 和S5B 等便对于以上提到的相应的具有常论域的模型类为完备的。
(通称巴坎公式)加入l 而得的新系统。此时,量词系统TB、S4B 和S5B 等便对于以上提到的相应的具有常论域的模型类为完备的。
以上这些事实均是在60年代以来获得的,这些结果显然促使人们把古典模型论中的典型定理推广和移植到模态逻辑中去。自70年代中期以来,K.A.鲍恩在这方面作了大量的工作。他成功地把古典模型论中的许多重要结果推广和移植到模态逻辑中。他所著的《模态模型论》一书可以说是集大成的著作。但是他的这些工作却受到了另一位模态模型论专家K.范因的尖锐批评。这些批评主要有两点:
(1)鲍恩的那些工作没有哲学意义;
(2)古典模型论中的许多标准定理不能推广和移植过去。这些定理包括E.W.贝思的可定义性定理(从而也包括克瑞格型的内插引理)以及S.谢拉赫的关于初等等价模型具有同构的超幂的定理等。 范因已经证明对于包括量词逻辑S5及S5B 在内的许多模态谓词逻辑,贝特型可定义性定理(从而也包括克瑞格型内插引理)均不成立;同时还指出谢拉赫的上述定理对S5B成立,而对量词逻辑S5 则失败,象这样的否定性结果还不断地出现。范因认为模态模型论的首要任务是作出具有哲学意义的模型论结果,而推广和移植古典模型论的定理只有在能用来帮助建立这些有哲学意义的结果的时候才是可取的。范因在模态模型论中获得的一个重要结果就是:dere怀疑主义和反哈耶塞特主义至少对于一阶模态语言而论是重合的。范因曾指出,他的这一定理,从逻辑上讲是古典模型论中所谓的保存定理的一个例子。
应该指出的是,鲍恩所著的《模态模型论》一书中错误甚多,特别是其中的鲁宾孙型联合无矛盾性引理,克瑞格型内插引理和贝特型可定义性定理象范因指出的那样,均不成立。
- 参考书目
- K.G.E.Hughes and M.J.Cresswell,An Introductionto Modal Logic,Methuen, London, 1968.
- K.K.A.Bowen,Model Theory for Modal Logic,D.Reidel Pub. Co., Dordrecht-Holland, 1979.