模型论

[拼音]：moxinglun

[外文]：model theory

数理逻辑的一个分支，是研究形式语言及其解释(模型)之间的关系的理论。在20世纪20年代，A.T.斯科朗等人在数理逻辑研究中就已得到模型论性质的重要结果；但作为系统的理论，模型论的奠基人应推A.塔尔斯基;后来A.鲁宾孙也对模型论作过较多贡献。在这方面有贡献的数学家主要还有R.L.沃特、A.И.马尔采夫、张晨钟、H.J.基斯勒、M.莫利、S.谢拉赫等人。

一个形式语言L的解释U称为此语言的一个模型或结构。U是一个具有若干运算、关系及特指元素的非空集合，也称为泛代数。所以，模型论又被形容为”泛代数＋逻辑“。由于所涉及的逻辑系统不同，模型论可分为：一阶模型论、高阶模型论、无穷长语言模型论、模态模型论、具有广义量词逻辑的模型论、多值模型论等。由于在数理逻辑中以一阶逻辑发展最成熟，所以，模型论也是以一阶模型论内容最丰富，应用也最多。

模型论与数理逻辑的其他分支（逻辑演算、证明论、递归论、公理集合论等）有着密切的联系。首先，各种逻辑演算是模型论的基础。此外，在证明论中，有关判定问题的研究广泛使用着模型论方法。在公理集合论中，有关大基数的研究与模型论有密切的联系。另外，布尔值模型被应用于各种独立性问题的研究。又如，递归论中很多重要概念及结果被推广应用于研究各种代数结构（模型），公理集合论中的力迫方法也被移植于模型论中，等等。

模型论中的概念与方法，除了主要来源于数理逻辑之外，也有不少来源于代数，它与抽象代数，特别是与泛代数理论的联系很密切。另外，由鲁宾孙所创始的非标准分析，则是模型论与分析数学相结合的产物。模型论与其他数学学科，例如数论、拓扑学、概率论等也有联系。在不少场合，模型论的成果不但是作为数学性的结论起作用，并且是作为逻辑性的结论而起着推理工具的作用。

一阶模型论

首先，所谓一阶语言，就是用狭义谓词演算范围内的逻辑概念所表达的语言。具体地说，也就是用个体变元、个体常元、函数符号、关系符号（或称谓词符号，一般包括等号在内）、与、或、非、蕴涵等命题连接词，以及“存在一个体”、“对一切个体”两个量词所表达的语言，例如代数中群、环、域的公理。其特点是，量词“存在”、“对一切”只允许对个体使用，而不许对集合、函数、关系等使用。

一阶模型论中一个基础性的定理是，如果一阶语言中一个命题集（即形式理论）T的每一有限子集都有模型，则T自身有模型。这个定理称为紧致性定理，它建立在一阶逻辑中著名的完备性定理之上。后者首先由K.哥德尔证明又经马尔采夫推广及L.亨金等给出新证法。亨金的证法后来被发展为模型论中构作模型的重要方法。紧致性定理的应用很广。例如，非标准分析的基础是实数系的非标准模型，其存在性就是根据紧致性定理或是它在高阶语言中的某种变形。

模型论中一个发现较早的重要定理是勒文海姆－斯科朗定理，它的内容发展了的含意是：设一阶语言L中所能表达的命题个数为λ（是一个超限数），如果L中的一个形式理论T有无限模型，则T有基数为任何α≥λ的模型。这个定理，在模型论及公理集合论中常被使用。

在对于模型的一阶性质的研究中，初等子模型及初等链是重要的概念及方法。与此有关的还有形式理论的模型完备性等概念及其对代数的应用。

如果一个形式理论T 的任何两个模型都具有完全相同的一阶性质，则称T 为完备的。在模型论中，可数完备理论的研究是一个比较系统而带有典型性的部分。例如，对于可数完备理论T，沃特得到了：T具有合理意义下的可数“小”模型（称为原子模型）的充分必要条件和T具有可数“大”模型（称为ω-饱和模型）的充分必要条件。 C.赖尔-纳尔德泽夫斯基等得到了 T 只有一个可数模型的充分必要条件。另外，沃特还有如下的有趣定理：T不会恰有两个不同构的可数模型。

斯科朗函数及不可辨元在构作模型时是有用的方法。例如，紧致性定理就可以用斯科朗函数来证明。又如，用它们可以证明：任何无限模型都具有任意大自同构群的初等扩张。

超积是模型论中一个重要的由已知模型构作新模型的方法。

饱和模型是模型论中一个重要概念，它是一种内部性质极丰富的有用的模型。例如，利用饱和模型可以比较一致地证明关于形式理论的各种保持性定理。又如，在下述莫利定理的证明中以及E.阿廷的一个猜想的证明中，都用到饱和模型。

一个形式理论T，如果它的任何两个基数为α 的模型都是同构的，则称T 为α 范畴的。莫利关于范畴性的一个著名定理是：对于可数语言中的完备理论T)，如果它对于一个不可数基数α 是α 范畴的，则T 对于任何不可数基数β 也是β 范畴的。范畴性是一个很有用的概念。一些模型论学者利用范畴性及另一个重要概念稳定性，对于群、环、域等代数结构进行了富有成果的研究。另外，谢拉赫在形式理论的稳定性及模型个数方面有深入的研究。谢拉赫还解决了在一大类无穷长语言中完备理论的模型个数问题。

马尔采夫和他的学生们，在模型论对代数的应用方面做了不少工作。他是这方面的创始人之一。

模型完备性

设ц是形式语言L的一个模型，B是ц的一个子模型。如果对B的每一n元组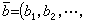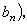(n=1，2，3，…)，姼在ц中及B中具有完全相同的一阶性质，则称 B为ц的初等子模型。设T 是L中的形式理论，如果T 的每一模型ц的每一子模型B当它适合T 时必是ц的初等子模型，则称T 为模型完备的理论。

初等子模型是塔尔斯基与沃特在20世纪50年代首先研究的。他们并且提出了初等链这一有效的模型构作方法。与此同时，鲁宾孙从代数中抽象出模型完备性的概念，并将此概念及模型论方法应用于代数问题的研究。到60年代，这方面已有不少成果。例如，可以证明代数闭域理论是模型完备的，并可由此得出希尔伯特零点定理的一个新证法。又如，可以证明实闭有序域理论是模型完备的，鲁宾孙并由此重新证明了阿廷等对希尔伯特第17问题的解答。

自70年代以来，鲁宾孙等人进一步发展了这方面的研究。他提出了形式理论的模型完备化及一些有关概念，并借鉴公理集合论中的力迫方法而提出一种模型论力迫法。又经过A.麦金太尔，谢拉赫等不少人的有关工作，使这方面的研究得到更深入的发展以及对代数方面新的应用。

例如，对于有限生成的群得到了它具有递归可解字问题的充分必要条件；对于微分域得到一种微分闭包的概念并证明了这种闭包的惟一性。

超积

超积的思想起源于斯科朗，到50年代由于J.沃希作了系统的奠基工作而开始在模型论及其他数学分支中起了重要作用。

超积概念建立在超滤子基础上，后者的定义如下:设I 为一非空集合，D是I的一些子集所成的集合。如果D 适合下列条件①～③，则称D为I上的一个滤子。

（1）I∈D，═唘D(═为空集)。

（2）若X，Y∈D，则X ∩Y∈D。

（3）若X ∈D且X嶅Y嶅I，则Y∈D。如果除此之外D又适合条件④对每一X嶅I，或X∈D，或I-X∈D，则称D为I上的一个超滤子。超滤子的存在性是容易证明的。

为使超积的定义叙述简便，以作可数多个域F₁，F₂，F₃，…的超积为例。以I记这些F_i的足标构成的集{1，2，3，…}，并设D 为I上的任一个超滤子。考虑一切无限序列(α₁，α₂，α₃，…)(α_i∈F_i)。依自然方式定义序列间的加法和乘法（即按分量相加、相乘），并如下定义序列间的关系“～”:(α₁，α₂，α₃，…)～(b₁，b₂，b₃，…)当且仅当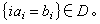由超滤子的性质易证“～”是一等价关系，并能保持＋，×运算。因而，可以在这些序列的等价类之间依自然方式导出＋，×运算而得到一个模型П_DF_i，称为诸F_i以D 为模的超积。容易证明它仍是一个域。特别地，若F₁=F₂=F₃=…=F，那么称超积П_DF_i为F的超幂。

一般模型的超积概念可以仿此定义。

超积П_DF_i的主要特性是：它能保持“几乎所有”F_i所共有的一阶性质。更准确地说就是：设 ψ是任意一个关于域的一阶性质，则П_DF_i适合ψ 的充分必要条件是{i｜F_i适合ψ}∈D。

一般模型的超积也有类似的特性。它被称为超积基本定理，是由沃希得到的。这一特性，是使超积在各种数学问题中起独特作用的基础。

在模型论中，超积常常能代替重要的紧致性定理而起到类似的作用。另外，利用超幂可以沟通模型的初等等价及同构这两个基本概念，谢拉赫证明了：语言L的两个模型ц、B初等等价的充分必要条件是它们具有同构的超幂。

在公理集合论中，超积与大基数（例如可测基数）的研究有密切联系。

超积在代数中有不少应用。一个著名的例子是：J.阿克斯与S.B.科琴以及 ю.Л.叶尔绍夫把超积以及饱和模型等模型论工具应用于赋值域的研究，正面解决了有理数域的p进赋值完全化域Q_p上的阿廷猜想。

在非标准分析以及起源于斯科朗的非标准算术中，其基础的数系可以采用由普通数系作超幂而得到的非标准数系，而超积基本定理则是沟通普通数系与非标准数系的桥梁。

以上举例介绍了一阶模型论的一些内容。模型论是一个年轻的数学分支，它还在迅速发展中，新概念新方法不断出现。特别是，它向代数、分析等数学学科中深入联系的趋势很明显。可以预料，随着模型论的不断发展，它将为其他数学分支提供更多的新工具和新方法。

参考书目

1. C.C.Chang and H.J.Keisler，Model Theory，2nded.，North-Holland， Amsterdam， 1976.