[拼音]:xianxingxing
[外文]:linear form
又称线性函数或线性齐式,是域F上的线性空间V到域F上的一个线性映射。如果ƒ是从V到F的映射,对V的向量尣、y,F的元素α、b满足ƒ(α尣+by=αƒ(尣)+bƒ(y),那么ƒ就称为V上的线性型或线性映射。若e1,e2,…,en是V 的一组基,则V 的每一个向量尣 都可表成
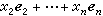 ,式中xi在F中,i=1,2,…,n。因此对于V上的线性型ƒ 有
,式中xi在F中,i=1,2,…,n。因此对于V上的线性型ƒ 有 或记成
或记成 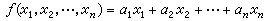 ,式中记ƒ(ej)=αj,i=1,2,…,n。若x 视为V 中的变元,则x1,x2,…,xn就可看作取值于F 的变元。因此,在基{e1,e2,…,en}之下,线性型ƒ就是F上n个变元的线性齐次函数。当V的基取定时,ƒ就由Fn的一个n元向量(α1,α2,…,αn)惟一确定。 V上的线性型全体按通常的函数加法与纯量乘法构成F上的一个线性空间,且与Fn同构。
,式中记ƒ(ej)=αj,i=1,2,…,n。若x 视为V 中的变元,则x1,x2,…,xn就可看作取值于F 的变元。因此,在基{e1,e2,…,en}之下,线性型ƒ就是F上n个变元的线性齐次函数。当V的基取定时,ƒ就由Fn的一个n元向量(α1,α2,…,αn)惟一确定。 V上的线性型全体按通常的函数加法与纯量乘法构成F上的一个线性空间,且与Fn同构。
如果V1、V2都是F上的线性空间,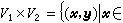
 是V1与V2的笛卡儿积,从V1×V2到F的映射φ,对于V1的向量尣,尣1,尣2;V2 的向量y,y1,y2;F的元素α1,α2,b1,b2,满足
是V1与V2的笛卡儿积,从V1×V2到F的映射φ,对于V1的向量尣,尣1,尣2;V2 的向量y,y1,y2;F的元素α1,α2,b1,b2,满足
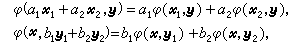
那么φ称为V1与V2上(或V1×V2上)的双线性型,或双线性函数或双线性齐式或双线性映射。若e1,e2,…,em与ƒ1,ƒ2,…,ƒn分别为V1与V2的基,
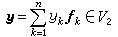 ,则
,则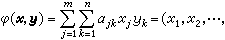
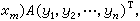 式中
式中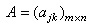 在F
在F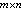 中,
中,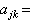
 由此可知,φ由矩阵A惟一确定,且可视为F上的两组变元x1,x2,…,xm与y1,y2,…,yn的双线性齐次函数。在V1与V2的基都选定时,V1×V2上的双线性型全体按通常的函数加法与纯量乘法组成一个F上的mn维线性空间,且与Fm×n同构。当V1与V2的基都改变时,V1×V2上的双线性型φ对应的矩阵,就变成由相应的演化矩阵惟一确定的等价矩阵。例如,
由此可知,φ由矩阵A惟一确定,且可视为F上的两组变元x1,x2,…,xm与y1,y2,…,yn的双线性齐次函数。在V1与V2的基都选定时,V1×V2上的双线性型全体按通常的函数加法与纯量乘法组成一个F上的mn维线性空间,且与Fm×n同构。当V1与V2的基都改变时,V1×V2上的双线性型φ对应的矩阵,就变成由相应的演化矩阵惟一确定的等价矩阵。例如,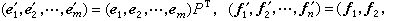
 这里p和Q分别为F上的m阶和n阶方阵,由坐标变换公式:
这里p和Q分别为F上的m阶和n阶方阵,由坐标变换公式:
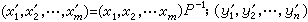
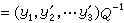
可得


因此,B=pAQT,式中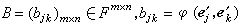 。j=1,2,…,m;k=1,2,…,n。对于V1与V2的任意基,φ所对应的矩阵有相同的秩,这个公共的秩称为 φ的秩,记为rankφ。当rankφ=r时,φ的标准形式(即在V1与V2的某基下φ的最简单形式)为
。j=1,2,…,m;k=1,2,…,n。对于V1与V2的任意基,φ所对应的矩阵有相同的秩,这个公共的秩称为 φ的秩,记为rankφ。当rankφ=r时,φ的标准形式(即在V1与V2的某基下φ的最简单形式)为
 , (1)
, (1)
此即表明,对两组旧变元x1,x2,…,xm与y1,y2,…,yn,总可经满秩的线性变换,使φ对两组新变元x媹,x崉,…,x怬与y媹,y崉,…,y怽取(1)的形式。
在V1=V2=V时,若双线性型φ对于V的任意向量尣、y有φ(尣,y)=φ(y,尣),则φ称为对称双线性型;若有φ(尣,y)=-φ(y,尣),则φ称为反对称双线性型。当V的基取定时,对称双线性型所对应的矩阵 A必为对称矩阵;反对称双线性型所对应的矩阵必为反对称矩阵。当V的基改变时,对称双线性型对应的矩阵A变为它的合同矩阵B=pApT,因此,可用对称矩阵的性质全面地描述对称双线性型的标准型等性质。例如,F=实数域 R,于是,每个实对称双线性型在正交变换(即 p为正交矩阵)下都可化为实正交标准型
 ,
,
式中λ1,λ2,…,λr是φ在任意基下对应的矩阵A的全体非零特征值。在复数域 C上,若只要求线性变换为满秩的,则它的标准型如 (1)所示。反对称双线性型可用反对称矩阵的性质描述和研究。
域F上的k个线性空间 V1,V2,…,Vk的笛卡儿积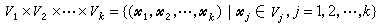 ,按通常的向量加法和纯量乘法成为 F上的一个线性空间,若
,按通常的向量加法和纯量乘法成为 F上的一个线性空间,若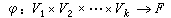 ,若对j=1,2,…,k满足
,若对j=1,2,…,k满足
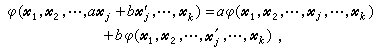
式中尣l∈Vl,l=1,2,…,k;尣徾∈Vj,α、b∈F, 则φ称为V1×V2×…×Vk上的k重线性型或k重线性映射。当k≥3时统称为多重线性型。
域F上的线性空间V的全体线性型,按通常的函数加法与纯量乘法,是F上的一个线性空间,记为V*。V*称为V的对偶空间,又称为V的关联空间或共轭空间。可以证明,当diтV是有限时,则diтV=diтV*。因此,V≌V*。这一结果在diт V是无限时不再成立。如果V的基{ej}与V*的基  式中δjk为克罗内克符号,那么这两组基底称为对偶基。用对偶基来描述线性型是很简单的。
式中δjk为克罗内克符号,那么这两组基底称为对偶基。用对偶基来描述线性型是很简单的。
若在域F上的k个线性空间V1,V2,…,Vk中,一些线性空间是另一些线性空间的对偶空间,则可引入混合张量的概念(见多重线性代数)。线性型已成为线性代数的一个重要内容。