[拼音]:zuixiao erchengfa
[外文]:method of least square
测量工作和科学实验中常用的一种数据处理方法,由A.-M.勒让德和C.F.高斯于19世纪初分别独立提出。例如,根据实验观测得到的自变量x和因变量y之间的一组对应关系(x1,y1),(x2,y2),…,(xm,ym),找出一个给定类型的函数y=ƒ(x)(如线性函数y=αx+b)或二次函数y=αx2+b)x+с等),使它在观测点x1,x2,…,xm处所取的值ƒ(x1),ƒ(x2),…,ƒ(xm)与观测值y1,y2,…,ym在某种尺度下最接近。常用的一种尺度和处理方法是:确定函数ƒ(x)中的参数(如前述例子中的参数α和b)或α、b)和с),使在各点处偏差
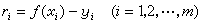
的平方和  达到最小。如果ƒ(x)是所有待定参数的线性函数(譬如ƒ(x)是多项式或其他已知函数的线性组合),相应的问题称为线性最小二乘问题。工程技术和科学实验中有大量利用最小二乘法建立的经验公式。
达到最小。如果ƒ(x)是所有待定参数的线性函数(譬如ƒ(x)是多项式或其他已知函数的线性组合),相应的问题称为线性最小二乘问题。工程技术和科学实验中有大量利用最小二乘法建立的经验公式。
从几何意义上讲,上述问题等价于确定一平面曲线(类型先给定),使它和实验数据点“最接近”,故又称为曲线拟合问题。它和插值法不同,并不要求曲线严格通过已知点。由于实验数据常带有观测误差和其他随机因素,所以与实验数据保持一致的插值法往往反倒不如最小二乘法得到的曲线更符合客观实际。
线性最小二乘问题设 ,其中α1,α2,…,αn为待定参数;φ1,φ2,…,φn为选定的已知函数(当
,其中α1,α2,…,αn为待定参数;φ1,φ2,…,φn为选定的已知函数(当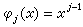 时,ƒ(x)为多项式)。实验数据为(x1,y1),(x2,y2),…,(xm,ym)。通常m比n大得多。令
时,ƒ(x)为多项式)。实验数据为(x1,y1),(x2,y2),…,(xm,ym)。通常m比n大得多。令 (i=1,2,…,m;j=1,2,…,n),并以C 表示以сij为元素的m×n阶矩阵,
(i=1,2,…,m;j=1,2,…,n),并以C 表示以сij为元素的m×n阶矩阵,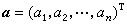 和
和 分别为n和m 维列向量,用这样的矩阵及向量记号,最小二乘问题可表为:求向量
分别为n和m 维列向量,用这样的矩阵及向量记号,最小二乘问题可表为:求向量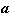 ,使
,使
 , (1)
, (1)
式中记号‖·‖2表示向量的欧氏长度。 由微分学求极小值的方法可推得待定参数,α1,α2,…,αn满足方程组
 。 (2)
。 (2)
这个方程称为最小二乘问题的法方程,它的解即为最小二乘解。如果C 为列满秩(即它的列向量线性无关),则CTC为非奇异的n×n阶矩阵,而方程组(2)有惟一解。如果C不是列满秩,则(2)的解不惟一。但具有最小欧氏长度的解是惟一的,这个解称之为极小最小二乘解。以C+表示C的穆尔-彭罗斯广义逆矩阵(见广义逆矩阵),则不论哪种情况,最小二乘问题(1)的解可表为
 。
。
当m较大时(实际问题多如此),CTC 往往是病态矩阵,因而从法方程(2)求最小二乘解是不利的。直接从矩阵C出发,进行所谓QR分解,则不仅可避免上述弊端,而且具有较好的数值稳定性。这个方法的原理是:对任意m×n阶矩阵C, 存在m×m 阶正交阵Q,使
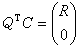 ,
,
式中R是n×n阶上三角阵。当C为列满秩时,R是非奇异的。由于在正交变换下向量的欧氏长度不变,所以
 (3)
(3)
式中y壒和y壗分别表示向量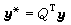 的前 n个分量和后(m-n)个分量所组成的向量。从(3)可看出方程
的前 n个分量和后(m-n)个分量所组成的向量。从(3)可看出方程

的解正是所求的最小二乘解。矩阵C 的QR分解,也就是阵矩QT的形成,可用一系列的豪斯霍尔德变换来实现。
- 参考书目