[拼音]:Lebeige jifen
[外文]:Lebesgue integral
黎曼积分的重要推广,分析数学中普遍使用的重要工具。
19世纪的微积分学中已经有了许多直观而有用的积分,例如黎曼积分(简称R积分)、黎曼-斯蒂尔杰斯积分(简称R-S积分)等。只要相应的函数性质良好,用这些积分来计算曲边形面积、物体重心、物理学上的功、能等,是很方便的。然而,随着认识的深入,人们愈来愈经常地需要处理复杂的函数,例如,由一列性质良好的函数组成级数所定义出来的函数,两个变元的函数对一个变元积分后所得到的一元函数等。在讨论它们的可积性、连续性、可微性时,经常遇到积分与极限能否交换顺序的问题。通常只有在很强的假设下才能对这问题作出肯定的回答。因此,在理论和应用上都迫切要求建立一种新的积分,它既能保持R积分的几何直观和计算上的有效,又能在积分与极限交换顺序的条件上有较大的改善。1902年法国数学家H.L.勒贝格出色地完成了这一工作,建立了以后人们称之为勒贝格积分的理论,接着又综合R-S积分思想产生了勒贝格-斯蒂尔杰斯积分(简称l-S积分)。20世纪初又发展成建立在一般集合上的测度和积分的理论,简称测度论。
黎曼积分的回顾改进R积分的主要想法是要扩大可积函数类,使得原来是R可积函数,按新积分仍可积,且积分值相同,而许多原来不是R可积函数,能按新积分可积。若能合理地扩大可积函数类,也就必然能在积分与极限交换顺序的条件上有某种改进。典型的例子是著名的狄利克雷函数 ,式中
,式中 在有理数rn上取值为1,在[0,1]的其余点上的值都是零,和式“
在有理数rn上取值为1,在[0,1]的其余点上的值都是零,和式“ ”表示对[0,1]中一切有理数求和。显然,每个
”表示对[0,1]中一切有理数求和。显然,每个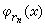 是R可积的,积分值是零,然而D(x)不是R可积的,自然更谈不上积分与级数求和交换顺序。但若有新的积分,使得D(x)可积,并且积分值是零,那么,
是R可积的,积分值是零,然而D(x)不是R可积的,自然更谈不上积分与级数求和交换顺序。但若有新的积分,使得D(x)可积,并且积分值是零,那么,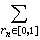
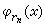 按新积分就可交换积分与求和的顺序。
按新积分就可交换积分与求和的顺序。
对于[α,b]上有界实函数ƒ(x)和[α, b]上任一分点组D:α=x0<x1<…<xn=b,作大、小和数


称 是ƒ(x)在[xi-1,xi]上的振幅。记
是ƒ(x)在[xi-1,xi]上的振幅。记
 。ƒ(x)在[α,b]上R可积的充分必要条件是
。ƒ(x)在[α,b]上R可积的充分必要条件是 ,或等价地,对任何η>0,
,或等价地,对任何η>0, 。这一条件揭示了R 可积函数的本质。D(x)在任何小区间[xi-1,xi]上振幅ωi=1,所以不是R可积的。如果考虑将分点组改在y轴上,例如,对于[α,b]上的有界实函数ƒ(x)(|ƒ(x)|<с),在[-с,с]上取分组点
。这一条件揭示了R 可积函数的本质。D(x)在任何小区间[xi-1,xi]上振幅ωi=1,所以不是R可积的。如果考虑将分点组改在y轴上,例如,对于[α,b]上的有界实函数ƒ(x)(|ƒ(x)|<с),在[-с,с]上取分组点 ,记
,记
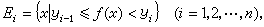

类似于R积分,作和式 ,式中
,式中 ,|Ei|表示集Ei的“长度”。这时,相应于D的大、小和数
,|Ei|表示集Ei的“长度”。这时,相应于D的大、小和数 与
与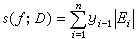 的差
的差 -
- ,将随着λ(D)趋于零而趋于零。这样就可以避免因函数在任何[xi-1,xi]上频繁振动而出现不可积的情况了。但这也产生了另外的问题:对于复杂的函数ƒ(x),相应的集Ei是否一定有“长度”|Ei|。因此,如要沿上述途径改进R积分,首先就要把过去只对区间有意义的长度概念推广到尽可能多的、复杂的集上去,这就导致了测度概念的出现。
,将随着λ(D)趋于零而趋于零。这样就可以避免因函数在任何[xi-1,xi]上频繁振动而出现不可积的情况了。但这也产生了另外的问题:对于复杂的函数ƒ(x),相应的集Ei是否一定有“长度”|Ei|。因此,如要沿上述途径改进R积分,首先就要把过去只对区间有意义的长度概念推广到尽可能多的、复杂的集上去,这就导致了测度概念的出现。
简称l测度,它是区间的长度、矩形的面积、长方体的体积的推广。
对于直线上的开集G,必存在惟一的有限个或可列个互不相交的开区间 ,使得
,使得 。利用这个事实,规定G的长度
。利用这个事实,规定G的长度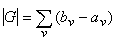 。再利用开集的长度,定义复杂点集的“长度”,即测度。设E是直线上任一点集,称
。再利用开集的长度,定义复杂点集的“长度”,即测度。设E是直线上任一点集,称 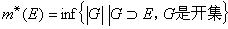 ,是E的外测度。m*(·)对直线上一切点集都有意义,但还不是长度的理想的推广,例如它不满足可加性(即对两个互不相交集E1和E2,m*(E1∪E2)并不一定等于m*(E1)+m*(E2))。如果一个点集E具有以下性质:对任何自然数n,存在开集Gn,使得Gn叾E,并且
,是E的外测度。m*(·)对直线上一切点集都有意义,但还不是长度的理想的推广,例如它不满足可加性(即对两个互不相交集E1和E2,m*(E1∪E2)并不一定等于m*(E1)+m*(E2))。如果一个点集E具有以下性质:对任何自然数n,存在开集Gn,使得Gn叾E,并且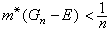 ,就称E是勒贝格可测集,简称l可测集。l可测集有很多等价定义方式)。直线上l可测集全体记为L。对于L中的E,定义m(E)=m*(E),称m(·)为(直线上的)l测度。m(·)是区间的长度在复杂的一类集(即L中的集)上的推广。L具有下列基本性质。
,就称E是勒贝格可测集,简称l可测集。l可测集有很多等价定义方式)。直线上l可测集全体记为L。对于L中的E,定义m(E)=m*(E),称m(·)为(直线上的)l测度。m(·)是区间的长度在复杂的一类集(即L中的集)上的推广。L具有下列基本性质。
(1)空集  、区间I、开集G、闭集都属于L,并且m(
、区间I、开集G、闭集都属于L,并且m( )=0,m(I)=|I|(|I|表示区间长度),m(G)=|G|。这样,有长度的集必在L中,并且其l测度就是长度。
)=0,m(I)=|I|(|I|表示区间长度),m(G)=|G|。这样,有长度的集必在L中,并且其l测度就是长度。
(2)可列可加性。如果{En}是L中一列互不相交的集,则 ,并且
,并且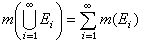 。
。
(3)如果E,F∈L,则E-F∈L。特别,当E叾F,并且m(F)<∞时,
m(E\F)=m(E)-m(F)。
利用以上三个基本性质,又可推出 L 的一系列其他性质,例如④有限可加性。当E1,E2,…,En∈L时,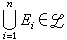 。再当E1,E2,…,En互不相交时,
。再当E1,E2,…,En互不相交时,
 。
。
(5)E∈L的充要条件是E的余集Ec(=(-∞,∞)- E)∈L。
(6)单调性。E,F∈L,当E叾F时,必有m(E)≥m(F)。
(7)次可列可加性。如果{En}是L中一列集,则 ,并且
,并且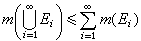 。
。
(8)单调极限交换性。设{En}是L中一列集,如果E1嶅E2嶅…嶅En嶅…,则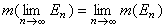 ;如果E1叾E2叾…叾En叾…,且m(E1)<∞,
;如果E1叾E2叾…叾En叾…,且m(E1)<∞,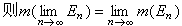 。
。
此外,L还具有⑨平移、反射不变性。如果E∈L,则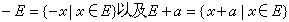 (α是任一实数)都属于L,并且m(-E)=m(E+α)=m(E)。
(α是任一实数)都属于L,并且m(-E)=m(E+α)=m(E)。
利用上述性质可以举出属于L的一些较复杂的集。例如,单点集{α}可视为[α,α],而且m([α, α])=0;直线上有理点全体Q 是可列集,由②可知Q∈L,并且m(Q)=0;由③可知,[0,1]上无理点全体D∈L,并且m(D)=1;再由 ①、③、⑦可知,直线上任何一列闭集的并集、一列开集的交集都在L中。实际上,直线上一切波莱尔集都在L中。
L可测集的判别判断直线上集E 是L 可测集的常用方法有如下几种。
(1)对任何ε>0,存在闭集F嶅E,使得m*(E-F)<ε。
(2)对任何ε>0,存在开集G,闭集F,使得G叾E叾F,且 m(G\F)<ε。
(3)对直线上任何集h,都有 ,这称做卡拉西奥多里条件。
,这称做卡拉西奥多里条件。
(4)仅当m*(E)<∞的情况,m*(E)=sup{m(F)|F嶅E,F是闭集}。这些条件中任何一个都可作为l可测集的定义。
勒贝格可测函数因为不是直线上所有集都是L可测的,所以不是每个函数ƒ(x)都具有下列性质:对任何y1<y2,集E={x|y1≤ƒ(x)<y2}都是l可测集。因此要 引入新的积分,还得引进可测函数概念。
设ƒ(x)是定义在l可测集M上的有限实值函数,如果对任何с<d, 集E={x|с≤ƒ(x)<d}是l可测集, 那么称ƒ(x)为M上的勒贝格可测函数,简称为l可测函数。常见的等价定义方式有:
(1)对任何实数с,E={x|ƒ(x)≥с}是l可测集。
(2)对任何实数с,E={x|ƒ(x)<с}是l可测集。
(3)对任何实数с,E={x|ƒ(x)≤с}是l可测集。
(4)对任何实数с,E={x|ƒ(x)>с}是l可测集。常用的一些函数,如[α, b]上连续函数、单调函数、阶梯函数、只有有限个或可列个不连续点的函数都是l可测的。[0,1]上的狄利克雷函数也是l可测的。
l可测函数有如下常用的基本性质。
(1)代数性质。如果ƒ,g是M上两个l 可测函数,那么αƒ+βg(α、β都是实数),max(ƒ, g),min(ƒ, g),|ƒ|,ƒg,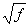 (当ƒ是非负函数),ƒ/g(当g不取零值)等都是l可测函数。
(当ƒ是非负函数),ƒ/g(当g不取零值)等都是l可测函数。
(2)极限性质。设{ƒn}是M上一列l可测函数,那么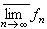 ,
, ,
,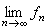 (只要它们处处有定义)都是l可测函数。
(只要它们处处有定义)都是l可测函数。
(3)l可测函数的结构(卢津定理)。如果ƒ是M上的l可测函数,那么对任何ε>0,必有(-∞,∞)上连续函数k,使得集E={x|ƒ(x)≠k(x),x∈M}的l 测度m(E)<ε。它是用连续函数刻画可测函数的深刻定理。
几乎处处“几乎处处”是测度和积分理论中的重要概念。设P是与集M中的点有关的命题,如果使命题P不成立的点的全体E 是l测度等于零的集,就称命题P在M上关于l测度m几乎处处成立。例如函数ƒ、h在M上关于m几乎处处相等,就是指集E={x|ƒ(x)≠h(x)}的l测度m(E)=0,记为 。依此就有狄利克雷函数
。依此就有狄利克雷函数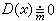 。又如函数列{ƒn}在M上关于m几乎处处收敛于ƒ,是指集
。又如函数列{ƒn}在M上关于m几乎处处收敛于ƒ,是指集 的 l测度m(E)=0,记为
的 l测度m(E)=0,记为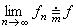 。有关“几乎处处”,l可测函数还有下列性质:如果
。有关“几乎处处”,l可测函数还有下列性质:如果 ,则ƒ与h同时是l可测或不可测函数;如果{ƒn}是M上一列l可测函数,且
,则ƒ与h同时是l可测或不可测函数;如果{ƒn}是M上一列l可测函数,且 ,则ƒ必是M上l可测函数。从积分的观点来看,几乎处处相等的函数可视为同一个函数。
,则ƒ必是M上l可测函数。从积分的观点来看,几乎处处相等的函数可视为同一个函数。
几乎处处收敛与一致收敛的差别显然很大,但它们之间仍有如下重要联系(叶戈罗夫定理):设{ƒn}是M上一列l可测函数,m(M)<∞。如果  ,那么,对任何δ>0,必存在M的l可测子集Eδ,使得m(M-Eδ)<δ,并且{ƒn}在Eδ上一致收敛于ƒ。
,那么,对任何δ>0,必存在M的l可测子集Eδ,使得m(M-Eδ)<δ,并且{ƒn}在Eδ上一致收敛于ƒ。
设M是l可测集,m(M)<∞,ƒ是M上有界可测函数,|ƒ(x)|<C,(C是正的常数)。任取分点组D: -C =y0<y1 <…<yn=C, 作和式 
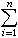
 。其中,
。其中,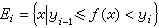 ,
,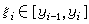 (i= 1, 2,…, n)。记
(i= 1, 2,…, n)。记 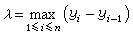 。如果存在
。如果存在 S(ƒ;D)=A,称ƒ在M上勒贝格可积,简称l可积,又称A是ƒ在M上的勒贝格积分,简称l积分,记为
S(ƒ;D)=A,称ƒ在M上勒贝格可积,简称l可积,又称A是ƒ在M上的勒贝格积分,简称l积分,记为 。当M 是区间 [α,b] 时,也记
。当M 是区间 [α,b] 时,也记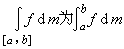 ,也常用
,也常用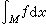 、
、 等来表示。
等来表示。
l积分具有如下性质。
(1)当m(M)<∞时,M上任何有界的l可测函数都是l可积的。特别,狄利克雷函数D(x)是l可积的,并且 。
。
(2)[α,b]上R可积函数ƒ(它必是有界的)必是l可积的,并且两种积分值相同。
(3)如果E是l可测集(m(E)可以无限大),ƒ是E上非负l可测函数,{En}是满足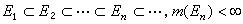 ,并且
,并且 的一列l 可测集,又{αn}是单调上升趋向无限大的数列,记
的一列l 可测集,又{αn}是单调上升趋向无限大的数列,记  ,那么极限
,那么极限
 与 {En}及{αn}的选取无关。另外,利用③可以定义一般的l可测集E上l可测函数ƒ 的l积分:当ƒ是E上非负l可测函数时,如果③中极限
与 {En}及{αn}的选取无关。另外,利用③可以定义一般的l可测集E上l可测函数ƒ 的l积分:当ƒ是E上非负l可测函数时,如果③中极限 是有限值,就称ƒ在E上l可积,并称这个极限值是ƒ在E上的l积分,记为
是有限值,就称ƒ在E上l可积,并称这个极限值是ƒ在E上的l积分,记为 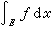 。当 ƒ是 E上一般l可测函数时,作
。当 ƒ是 E上一般l可测函数时,作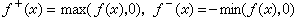 , ƒ+和 ƒ-都是非负的,并且ƒ=ƒ +-ƒ -。如果ƒ +,ƒ -都是E上l可积的,就称ƒ在E上l可积,并称
, ƒ+和 ƒ-都是非负的,并且ƒ=ƒ +-ƒ -。如果ƒ +,ƒ -都是E上l可积的,就称ƒ在E上l可积,并称 为ƒ在E上的l积分,仍记为
为ƒ在E上的l积分,仍记为 ,这就是直线上最一般的l积分概念。l积分还有如下常用性质。
,这就是直线上最一般的l积分概念。l积分还有如下常用性质。
(4)线性性质。当ƒ,g在E上l可积时,对任何两个实数α和β,αƒ+βg在E上必l可积,并且 。 ⑤如果
。 ⑤如果 在E上成立,则ƒ在E上l可积的充要条件是g在E上l可积。当ƒ可积时,有
在E上成立,则ƒ在E上l可积的充要条件是g在E上l可积。当ƒ可积时,有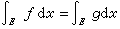 。
。
(6)单调性。如果ƒ,g在E上都是l可积的,并且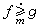 ,则
,则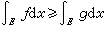 。特别,非负函数的l积分必是非负值。
。特别,非负函数的l积分必是非负值。
(7)如果非负函数ƒ的积分 ,则必在E上
,则必在E上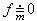 。
。
(8)绝对可积性。ƒ在E上l可积的充分必要条件是|ƒ|在E上l可积,并且有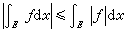 。
。
(9)可列可加性。设{Ei}是一列互不相交的l可测集,则ƒ在 上l可积的充要条件是ƒ在每个Ei上l可积,并且
上l可积的充要条件是ƒ在每个Ei上l可积,并且 。当ƒ在
。当ƒ在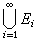 上l可积时,
上l可积时,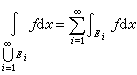 。
。
(10)全连续性(绝对连续性)。设ƒ在E上l可积,则对任何ε>0,必存在δ>0, 只要E中l可测集e满足m(e)<δ, 就有 。积分逼近。如果ƒ是E上l可积函数, 则对任何ε>0,必有(-∞,∞)上连续函数h,阶梯函数φ,使得
。积分逼近。如果ƒ是E上l可积函数, 则对任何ε>0,必有(-∞,∞)上连续函数h,阶梯函数φ,使得
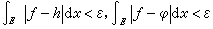 。
。
下面是经常用的三个重要极限定理。列维引理。设{ƒn}是E上一列l可积函数,且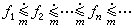 。如果
。如果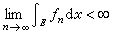 ,则{ƒn}必在E上关于m几乎处处收敛于某个l可积函数ƒ,并且
,则{ƒn}必在E上关于m几乎处处收敛于某个l可积函数ƒ,并且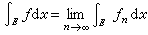 。法图引理。设{ƒn}是E上一列l可积函数,如果有E上l可积函数h,使得
。法图引理。设{ƒn}是E上一列l可积函数,如果有E上l可积函数h,使得 ,且
,且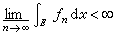 ,则
,则 必在E 上l 可积, 并且
必在E 上l 可积, 并且 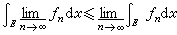 。勒贝格控制收敛定理。设 {ƒn} 是E 上一列 l可积函数,如果有E上l可积函数F,使得
。勒贝格控制收敛定理。设 {ƒn} 是E 上一列 l可积函数,如果有E上l可积函数F,使得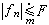 (n=1,2,…),且{ƒn}在E上关于m几乎处处收敛于ƒ,则ƒ必在E上l可积,且
(n=1,2,…),且{ƒn}在E上关于m几乎处处收敛于ƒ,则ƒ必在E上l可积,且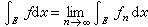 。上述三个定理是等价的,即其中之一成立,另两个也必成立。较更常用。
。上述三个定理是等价的,即其中之一成立,另两个也必成立。较更常用。
此外,l积分还有一个重要性质。平移、反射不变性。如果ƒ在(-∞,∞)上l可积,则对任何实数α,ƒ(x+α)及 ƒ(-x) 都在 (-∞,∞)上l可积,且
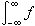

 。积分的平移、反射不变性产生于l测度的平移、反射不变性,它是建立调和分析理论的基础。
。积分的平移、反射不变性产生于l测度的平移、反射不变性,它是建立调和分析理论的基础。
在处理积分与极限交换顺序问题上,l积分所要求的条件(、、中的条件)比R积分所要求的条件(通常是一致收敛)弱得多,因此l积分远比R积分有效。利用l积分的极限定理,还可进一步揭示R可积函数的本质:[α,b]上有界函数ƒ(x)为R可积的充要条件是ƒ(x)的不连续点全体是l测度为零的集。
度量收敛和积分平均收敛在l积分理论中,除几乎处处收敛这一个重要收敛概念外,还有两个重要收敛概念。
(1)设{ƒn}是集E上一列l可测函数,如果存在E上函数ƒ,使得对任何 ,那么称{ƒn}在E上度量收敛或依测度收敛于ƒ。度量收敛在概率论中,具有特别重要的地位。下面是度量收敛的常用性质:设{ƒn}、{gn}是E上l可测函数列,并且分别度量收敛于ƒ和g,则ƒ和g必是E上l可测函数,并且对任何数α和β,
,那么称{ƒn}在E上度量收敛或依测度收敛于ƒ。度量收敛在概率论中,具有特别重要的地位。下面是度量收敛的常用性质:设{ƒn}、{gn}是E上l可测函数列,并且分别度量收敛于ƒ和g,则ƒ和g必是E上l可测函数,并且对任何数α和β, 在E上度量收敛于 αƒ+βg;如果进一步又假设m(E)<∞,则{ƒngn}在E上度量收敛于 ƒg,而当 gn(n=1,2,…)和g都是几乎处处不等于零的函数时,
在E上度量收敛于 αƒ+βg;如果进一步又假设m(E)<∞,则{ƒngn}在E上度量收敛于 ƒg,而当 gn(n=1,2,…)和g都是几乎处处不等于零的函数时,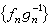 在E上度量收敛于ƒg-1(在gn或g取值等于零的点上可任意规定
在E上度量收敛于ƒg-1(在gn或g取值等于零的点上可任意规定 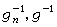 的值)。度量收敛和几乎处处收敛的关系如下:如果{ƒn}在E 上度量收敛于ƒ,那么必有子序列
的值)。度量收敛和几乎处处收敛的关系如下:如果{ƒn}在E 上度量收敛于ƒ,那么必有子序列 在E上几乎处处收敛于ƒ;当 m(E)<∞ 时,{ƒn}在E上几乎处处收敛于ƒ必也度量收敛于ƒ;而{ƒn}度量收敛于 ƒ当且仅当在任何子序列
在E上几乎处处收敛于ƒ;当 m(E)<∞ 时,{ƒn}在E上几乎处处收敛于ƒ必也度量收敛于ƒ;而{ƒn}度量收敛于 ƒ当且仅当在任何子序列  中还可找到在E上几乎处处收敛于ƒ 的子序列。
中还可找到在E上几乎处处收敛于ƒ 的子序列。
(2)设p>0,如果E上l可测函数ƒ(x)的 是l可积的,则称ƒ(x)为E上p次l可积函数。如果{ƒn}是E上一列p 次l可积函数,并且存在E上函数ƒ,使得
是l可积的,则称ƒ(x)为E上p次l可积函数。如果{ƒn}是E上一列p 次l可积函数,并且存在E上函数ƒ,使得 ,则称{ƒn}在E上p 次(积分)平均收敛于ƒ。当n=1,2时,分别简称为积分平均收敛、平方平均收敛。下面是 p次平均收敛常用的性质:设{ƒn}和{gn}在E上分别p次平均收敛于ƒ和g, 则 ƒ 和g必在 E上 p次l可积,并且对任何数α 和β,
,则称{ƒn}在E上p 次(积分)平均收敛于ƒ。当n=1,2时,分别简称为积分平均收敛、平方平均收敛。下面是 p次平均收敛常用的性质:设{ƒn}和{gn}在E上分别p次平均收敛于ƒ和g, 则 ƒ 和g必在 E上 p次l可积,并且对任何数α 和β,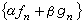 必在E上p次平均收敛于αƒ+βg;如果{ƒn}在E上p次平均收敛于ƒ,则必有子序列
必在E上p次平均收敛于αƒ+βg;如果{ƒn}在E上p次平均收敛于ƒ,则必有子序列 在E上度量收敛于ƒ,从而在
在E上度量收敛于ƒ,从而在 中又可以找到一个子序列关于m几乎处处收敛于ƒ,但逆命题不成立。
中又可以找到一个子序列关于m几乎处处收敛于ƒ,但逆命题不成立。
类似于柯西基本数列,可以引入如下概念:设{ƒn}是E上一列l可测函数(或p次L可积函数),如果对任何ε>0,
 -
- ,则称{ƒn}为E上的度量基本序列(或p 次平均基本序列)。和实数的完备性一样,有如下的完备性定理:如果{ƒn}是 E上的度量基本序列(或p 次平均基本序列),则必存在E上的l可测函数(或p 次可积函数)ƒ,使得{ƒn}度量收敛(或p次平均收敛)于ƒ。
,则称{ƒn}为E上的度量基本序列(或p 次平均基本序列)。和实数的完备性一样,有如下的完备性定理:如果{ƒn}是 E上的度量基本序列(或p 次平均基本序列),则必存在E上的l可测函数(或p 次可积函数)ƒ,使得{ƒn}度量收敛(或p次平均收敛)于ƒ。
类似于直线情况,从 n维空间长方体的“体积”出发可以引出 n维空间中一般点集的外测度、l可测集、l测度m、l可测函数、l积分等概念及其相应的性质。下面以二维空间的情形为例,设E是平面上点集,对每个数x,称集Ex={y|(x,y)∈E}为E在x的截口。同样,称Ey={x|(x,y)∈E}为E在y的截口。如果E是平面上l可测集,那么对于几乎所有的x(或y),Ex(或Ey)是y轴上(或 x轴上)的l可测集。如果 ƒ(x,y)是E 上的l 可测函数, 那么对于几乎所有的 x(或 y),ƒx(y)呏ƒ(x,y)(或ƒy(x)呏ƒ(x,y))是Ex(或Ey)上l可测函数。对于平面上l可测函数 ƒ(x,y),如果ƒ是平面上l可积的(其积分记作 ),则对几乎所有的x,ƒx(y)是y 轴上l可积函数,而函数
),则对几乎所有的x,ƒx(y)是y 轴上l可积函数,而函数
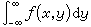 (在ƒx(y)不可积的x上,可任意规定ψ(x)的值)是x 轴上l 可积函数,且
(在ƒx(y)不可积的x上,可任意规定ψ(x)的值)是x 轴上l 可积函数,且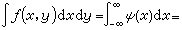
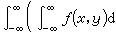
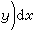 。 对调 x 和y地位,类似地也有
。 对调 x 和y地位,类似地也有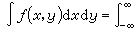
 dx。反之,如果对几乎所有的x,|ƒx(y)|=|ƒ(x,y)|是 y轴上l可积函数,并且
dx。反之,如果对几乎所有的x,|ƒx(y)|=|ƒ(x,y)|是 y轴上l可积函数,并且
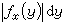 (对于|ƒx(y)|不可积的x,可任意规定φ(x)的值)也是x轴上l可积函数,则ƒ(x,y)是平面上l可积函数。因此,得到
(对于|ƒx(y)|不可积的x,可任意规定φ(x)的值)也是x轴上l可积函数,则ƒ(x,y)是平面上l可积函数。因此,得到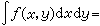

 ,这一结果被称为关于重积分和累次积分的富比尼定理。简单说,就是对n维空间都成立。重积分存在时,两个累次积分必存在,并且相等;反之,只要它的绝对值函数的一个累次积分存在,则重积分也就存在。
,这一结果被称为关于重积分和累次积分的富比尼定理。简单说,就是对n维空间都成立。重积分存在时,两个累次积分必存在,并且相等;反之,只要它的绝对值函数的一个累次积分存在,则重积分也就存在。
由黎曼积分发展出勒贝格积分,由黎曼-斯蒂尔杰斯积分就发展出勒贝格-斯蒂尔杰斯积分(简称为l-S积分)。 设g(x)是(-∞,∞)上单调增加的右连续函数。对于区间I规定它的g长度g(I)如下:g((α,b])=g(b)-g(α);g((α,b))=g(b-0)-g(α);g([α, b])= g(b)-g(α-0);g([α, b))=g(b-0)-g(α-0)。特别,当 g(x)呏x时,g长度就是普通长度。利用区间的g长度就可引入直线上开集G的g长度g(G),以及直线上任何点集E的g外测度
 。与引入l可测集、l测度一样,只要将m*换成g*,就可定义关于g的l-S可测集,其全体记为Lg。对于E∈Lg ,规定
。与引入l可测集、l测度一样,只要将m*换成g*,就可定义关于g的l-S可测集,其全体记为Lg。对于E∈Lg ,规定 , 称mg为由g(x)产生的l-S测度。同样,可以引入关于g的l-S可测函数和关于g的l-S积分。这些分别简称为关于g的测度,关于g的可测函数,关于g 的积分等。有关l可测集、l测度、l可测函数、l积分的一切性质除去平移、反射不变性以外, 对相应的关于g的可测集、测度、可测函数、积分也成立。
, 称mg为由g(x)产生的l-S测度。同样,可以引入关于g的l-S可测函数和关于g的l-S积分。这些分别简称为关于g的测度,关于g的可测函数,关于g 的积分等。有关l可测集、l测度、l可测函数、l积分的一切性质除去平移、反射不变性以外, 对相应的关于g的可测集、测度、可测函数、积分也成立。
建立高维空间上的 l-S积分理论,一般有两种方式。
(1)乘积测度形式。即设 g1(x),g2(x)是(-∞,∞)上两个单调增加右连续函数,利用它们可以规定“左开右闭”矩形J=(α,b]×(c,d]的 g1×g2面积:g1×g2(J)=g1((α,b])g2((с,d]),以及有限个互不相交的“左开右闭”矩形 J1,J2,…,Jn的并集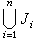 的 g1×g2面积:
的 g1×g2面积: ;利用它们引入平面上任何点集 E 的g1×g2 外测度
;利用它们引入平面上任何点集 E 的g1×g2 外测度 

 ,而J1,J2,…, Jn是互不相交的“左开右闭”矩形}。还可相应地引入 g1×g2可测集,测度
,而J1,J2,…, Jn是互不相交的“左开右闭”矩形}。还可相应地引入 g1×g2可测集,测度  ,可测函数和积分。和l积分一样,对关于 g1×g2 的积分也有重积分和累次积分的富比尼定理,只要将l积分的富比尼定理中x轴、y轴上的l测度分别换成测度
,可测函数和积分。和l积分一样,对关于 g1×g2 的积分也有重积分和累次积分的富比尼定理,只要将l积分的富比尼定理中x轴、y轴上的l测度分别换成测度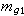 、
、 即可。
即可。
(2)一般形式。设φ(x,y)是平面上的函数,固定一个变元时,它是另一个变元的右连续函数。如果对任何区间 J = (α,b]×(с,d],值 
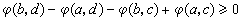 ,则称φ(J)为J 的φ面积。由此又可引入平面上任何一个集的φ 外测度φ*和相应的关于φ的可测集、测度m
,则称φ(J)为J 的φ面积。由此又可引入平面上任何一个集的φ 外测度φ*和相应的关于φ的可测集、测度m 、可测函数及积分。关于φ的积分,一般说来没有相应的富比尼定理。
、可测函数及积分。关于φ的积分,一般说来没有相应的富比尼定理。
如果给定直线上两个(或两个以上)单调增加右连续函数 g1(x),g2(x),这时相应地就有关于g1,g2的可测集,可测函数,积分等。对于直线上的点集E(或函数ƒ),可能会发生E(或ƒ)是关于g1可测的,但不是关于g2可测的。所以,在讨论的问题中如果有几个l-S测度、积分同时出现,就很不方便。这就要求有一集类(或一函数类),它一方面包含足够丰富的集(或函数),能够适应代数和极限运算的需要,另一方面它的每个集(或函数)对一切g来说都是可测的。适合这种要求的最理想的类就是波莱尔集类和波莱尔可测函数类(见贝尔函数)。
测度问题和不可测集以直线而论,人们总希望直线上的某个测度,关于它的可测集越多越好。可测集多,意味着可测函数多,从而可积函数也多。从调和分析看,l 测度平移不变性是建立调和分析基础。从逐项积分看,总希望测度具有可列可加性(它与控制收敛等极限定理等价)。所谓测度问题就是直线上是否存在具有下面性质的测度:
(1)具有可列可加性,②直线上所有子集都可测,③具有平移不变性,④[0,1]的测度是非零的有限值。这个问题已经完全解决。结论如下:去掉②、③、④中任何一条,满足其余三条的测度是容易举例说明其存在的。
(1)、②、③、④全都满足的测度是不存在的,特别,直线上必存在不是l可测的集。如果将①换成①′有限可加性,则满足①′、②、③、④的测度是存在的。