[拼音]：zhixian
[外文]：straight line
构成几何图形的最基本的元素。在D.希尔伯特建立的欧几里得几何的公理体系中(见欧几里得几何学)，把点、直线和平面与“点在直线上”、“点在平面内”、“一点在另两点之间”、“线段合同”、“角合同”一起作为基本概念，由“结合公理”、“顺序公理”、“合同公理”、“连续公理”、“平行公理”等五组公理制约。换句话说，它们的概念体现在这五组公理之中。
在建立了直角坐标系 Oxy的坐标平面内，直线的方程是x、y的一次方程。
如果把直线方程写成Ax+By+C=0（A、B不全为0）的形式，这种形式的直线方程，通常叫做直线方程的一般式。
通过定点M0（x0，y0）、斜率为k的直线的方程为y-y0=k(x-x0)。这种形式的直线方程，叫做直线方程的点斜式。当斜率为k的直线在y轴上的截距为b)时，直线的方程为y=kx+b)。这种形式的直线方程，叫做直线方程的斜截式。
通过两定点M1(x1，y1)和M2(x2，y2)的直线的方程为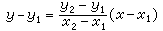
。这种形式的直线方程，叫做直线方程的两点式。当直线在x轴、y轴上的截距分别为α、b)时，直线的方程为
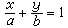。这种形式的直线方程，叫做直线方程的截距式。
方程为Ax+By+C＝0(A、B不全为0)的直线的斜率为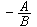
；在x轴、y轴上的截距分别为
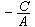和
。
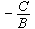由坐标原点O至直线l的距离如果为p(≥0)，直线l的法线l┡与x轴的正半轴的交角如果为θ(0≤θ<2π)(图1
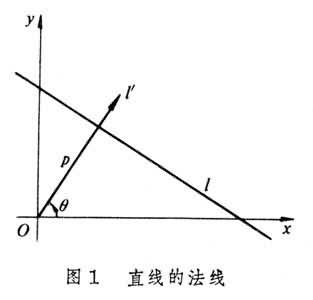
)，直线l的方程为x cosθ+y sinθ-p=0。这种形式的直线方程，通常叫做直线方程的法线式。
在同一直角坐标系Oxy中，如果一直线的方程的一般式为Ax+By+C＝0，方程的法线式为x cosθ+y sinθ-p＝0，那么
。
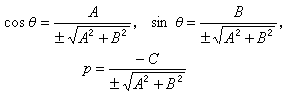
一直线x cosθ＋y sinθ-p＝0至一定点M0(x0，y0)的距离为d=x0cosθ＋y0sinθ－p。如果此直线方程为Ax+By+C＝0，那么，至点M0(x0，y0)的距离为
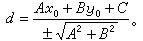
式中根式的符号与C的符号相反。
如果直线l1和l2的斜率分别为k1和k2（图2
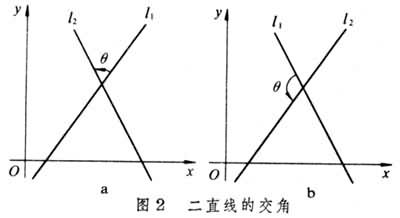
），l1和l2所指定的交角的正切为
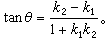
直线l1和l2平行的充要条件是k1=k2；垂直的充要条件是k1k2=-1或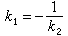
。
如果直线l1和l2的方程分别为A1x＋B1y＋C1＝0和A2x+B2y +C2=0，那么，l1和l2的交点坐标为
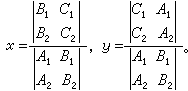
如果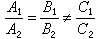
，那么，l1∥l2。如果
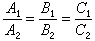，那么l1和l2重合。
如果以直角坐标系Oxy的原点O为极，Ox为极轴建立极坐标系，那么，在直角坐标系Oxy中，一直线的方程如果是x cosθ+y sinθ-p＝0，它在该极坐标系的方程即直线上点的极坐标(ρ，α)所满足的方程为
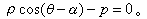
在直角坐标系Oxy中建立了坐标向量后，取一点M0，其向径为r0{x1，y1}，取任意非零向量n{A，B}，引垂直n并通过点M0的直线l。设M(x，y)是直线l上任意点(图3
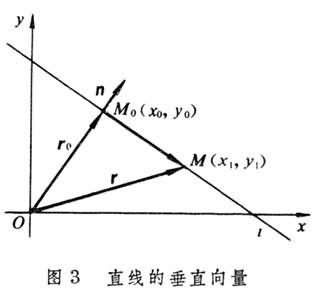
)，其向径为r{x，y}，那么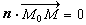
或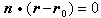
，就是直线l的向量方程。
设i、j分别为Ox、Oy轴的正方向上的单位向量，那么，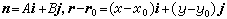
。因而
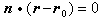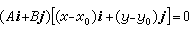，即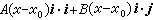
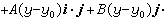
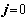;即
；即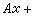
。
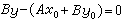设C＝-(Ax0＋By0)，上述方程即Ax＋By＋C＝0。因此，直线l的向量方程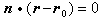
便化为直线方程的一般式。