[拼音]：hanshu de lianxuxing
[外文]：continuity of functions
描述函数的一种连绵不断变化的状态，即自变量的微小变动只会引起函数值的微小变动的情况。确切说来，函数在某点连续是指：当自变量趋于该点时，函数值的极限与函数在该点所取的值一致。
一元连续函数
设函数ƒ(x)在x＝α附近（包括x=α处）有定义。若
，
(*)亦即：对任给ε>0，必有δ>0存在，使当｜x-x0｜<δ时，恒有｜ƒ(x)-ƒ(α)｜<ε，则称ƒ(x)在x＝α处连续，α为ƒ(x)的连续点。
如在(*)中，x →α改为x →α-0或x →α+0，即限定x<α或x>α，则称ƒ(x)在x=α处左连续或右连续。显然ƒ(x)在x=α处连续的必要充分条件为它在α处左、右都连续。
如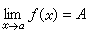
存在，但A≠ƒ(α)或 ƒ(α)没有意义，则称ƒ(x)在α处为可去间断（可去不连续），因为这时只要改变或补充定义ƒ(α)使其等于A就可使它变得在α处连续；因此，这种不连续常常算作是连续的。如果x→α时，则称ƒ(x)在α处有第一类间断，B-A称为其跃度。不属于上述情况的不连续点都称为第二类间断。
如果ƒ(x)在一开区间(α，b)内每一点都连续，则称ƒ(x)在开区间(α，b)内连续。ƒ(x)在一闭区间[α，b]上连续是指：在开区间(α，b)内连续，而在α处右连续和b处左连续。
由此可确切定义几何名词连续曲线。设平面曲线 C可写成参数方程
x =x(t)， y =y(t) (α≤t≤β)，
其中x(t)、y(t)都是[α，β]上的连续函数，则称C是连续曲线。此定义显然可推广到空间曲线甚至一般的 n维空间中的曲线上去。
连续函数的性质
（1）如ƒ(x)、g(x)都在x=α处连续，则ƒ(x)±g(x)，ƒ(x)g(x)，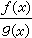
（只要g(α)≠0)也在x=α处连续。
（2）如ƒ(x)在x=α处连续，且ƒ(α)≠0，则必在x＝α的某一小δ邻域（即|x-α|<δ）中，ƒ(x)不变号，即ƒ(x)与ƒ(α)同号。
（3）在闭区间上的连续函数，必有上界和下界，且有最大值和最小值，并能取最小值和最大值之间的一切中间值。
还可证明，所有初等函数在其有定义的区间上都是连续的。
设I为一闭或开的区间，如果任给ε>0，必有δ>0存在，使对I中任何两点x，x′，只要|x-x′|<δ，便有｜ƒ(x)-ƒ(x′)|<ε，则称ƒ(x)在I上一致连续。关于一致连续性有下面的重要定理：在闭区间上的连续函数一定在该区间上一致连续。这一定理有时称作康托尔定理。
多元连续函数
设
为一 n元函数，这里x=(x1，x2，…，xn)为n维向量或n维空间中一点，而α=( α1，α2，…，αn)为一定点。如果(1)式成立，亦即对任给ε>0，必有δ>0存在，使当
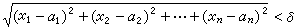
或者
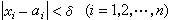
时，恒有
｜ƒ(x)-ƒ(α)｜<ε
，则称ƒ(x)在α处连续。也可类似地定义ƒ(x)在n维区域G中连续和一致连续。不过，当α是ƒ(x)定义域G边界上的一点时，在上面定义中要限制x在G及其边界上。
一元连续函数的上述性质都可推广到多元函数上来，康托尔定理这时也成立，不过在其中区间I要换成有界闭区域。和连续曲线类似，也可定义连续曲面等等。
以上连续函数的定义也可推广到复变量的复函数上来（见复变函数）。
连续函数的定义还可推广到一般抽象的拓扑空间的情况。设X，Y是两个拓扑空间，ƒ:X→Y是把X映入Y的一个映射，又α∈X，如果对于ƒ(α∈Y的任一邻域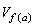
，存在着α的一邻域Uα，使
，
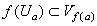则称ƒ在α点连续。如果ƒ在X中的每一点都连续，则称ƒ为X到Y的一连续映射。