[拼音]：Kexi jifen dingli
[外文]：Cauchy integral theorem
A.-L. 柯西研究复变函数的积分所得到的基本定理。应用这一定理可导出解析函数的一系列重要性质。例如，可证明如果一复变函数在一区域内是解析的(即有导数)，则其导数必连续且任意阶导数必存在；还可计算一些定积分或反常积分，等等。
复积分定义
设函数ƒ(z)=u+iv在可求长曲线Г上是连续的，其中u和v分别是ƒ(z)的实部和虚部。在Г上依次取分点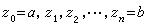
。Г上从zk-1到 zk的小段记为Гk，在Гk上任取一点
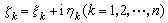，作和数
。
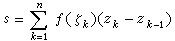如果当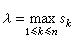
（sk是Гk的弧长）趋于零时，s趋于一极限值，则称这个极限值为ƒ(z)沿曲线Г的积分，记为
，
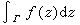即
。
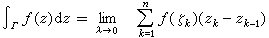因为
，
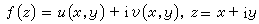所以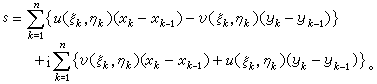
当λ→0时，上式右边的两个和数分别趋于
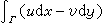
与
，
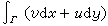于是有
。
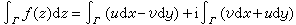柯西积分定理
设ƒ(z)在有限单连通区域（即“无洞”且不含无穷远点的区域）D内解析，Г是D内任一条可求长、简单（即本身不相交）、闭(即两端点重合)曲线，则
。
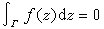柯西定理有一逆定理，即莫雷拉定理，这一定理与柯西积分定理相结合，可叙述为：设ƒ(z)在有限单连通区域D内连续，则ƒ(z)在D内解析的充分必要条件是：对D内任一条可求长简单闭曲线（或任一三角形）Г，
。
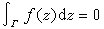柯西积分公式
由柯西积分定理可导出柯西积分公式，这一公式把解析函数用曲线积分表示出来。特别，它用解析函数在一闭曲线上的值，表示出它在曲线内侧的值。柯西积分公式可表述如下：设ƒ(z)在有限单连通区域D内解析，Г是D内任一条可求长简单闭曲线，则对Г所围区域内任一点z，
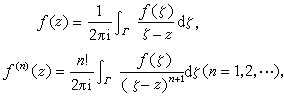
式中积分是在Г上沿反时针方向取的。
柯西积分公式启发人们研究柯西型积分。 设函数φ(ξ)在某一可求长简单闭曲线Г上可积(ξ∈Г)，则由柯西型积分
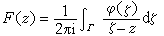
确定的函数， 当z媂Г时是解析的。对于Г上几乎所有的点z0，当z从Г的内侧及外侧沿不与Г相切的曲线分别趋近于z0时，有极限
，
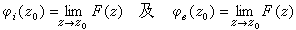式中
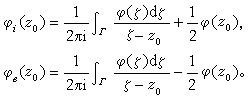
当Г不是闭曲线时，也有类似结果。柯西型积分可应用于研究解析函数的边界性质、边值问题及奇异积分方程。
引进同伦及同调概念，可以把柯西积分定理叙述成一般形式。设Г0:z=Г0(s)及Г1:z=Г1(s)(0≤s≤1)是区域D内两条可求长闭曲线，设存在着在D内取值的连续函数z=G(s，t)(0≤s≤1，0≤t≤1)，使得
G(s，0)= Г0(s)，G(s，1)=Г1(s) (0≤s≤1)；
G(0，t)=G(1，t) (0≤t≤1)，
则称Г0与Г1在D内同伦。
对于z媂Г0，定义z关于Г0的指标为
。
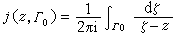如果D的余集中任何点关于Г0及Г1的指标相同，则称Г0及Г1在D内同调。可以证明，如果Г0及Г1在D内同伦，则它们也在D内同调。柯西积分定理的一般形式是:设ƒ(z)在区域D内解析，Г0和Г1是D内两条同伦或同调的可求长闭曲线，则
。
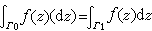