[拼音]：zhengshu fenchai
[外文]：Partition of integral number
堆垒数论的一个基本问题。把正整数 n分成为不计次序的若干个正整数之和
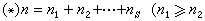
的一种表示法，称为n的一种分拆。对被加项及项数加以一些限制条件，就得到某种特殊类型的分拆，n的某类型所有不同的分拆个数r(n)，称为该类型分拆的分拆函数。通常根据情况约定 r(0)=0或1。对被加项的限制条件主要是关于它们的大小、它们的差的大小，以及它们属于某些指定的剩余类。不加限制条件的分拆，称为无限制分拆，其分拆函数记作p(n)，它是一类重要的分拆。例如，6=5+1=4+2=4+1+1=3+3=3+2+1=3+1+1+1=2+2+2=2+2+1+1=2+1+1+1+1=1+1+1+1+1+1， 所以p(6)=11。表1
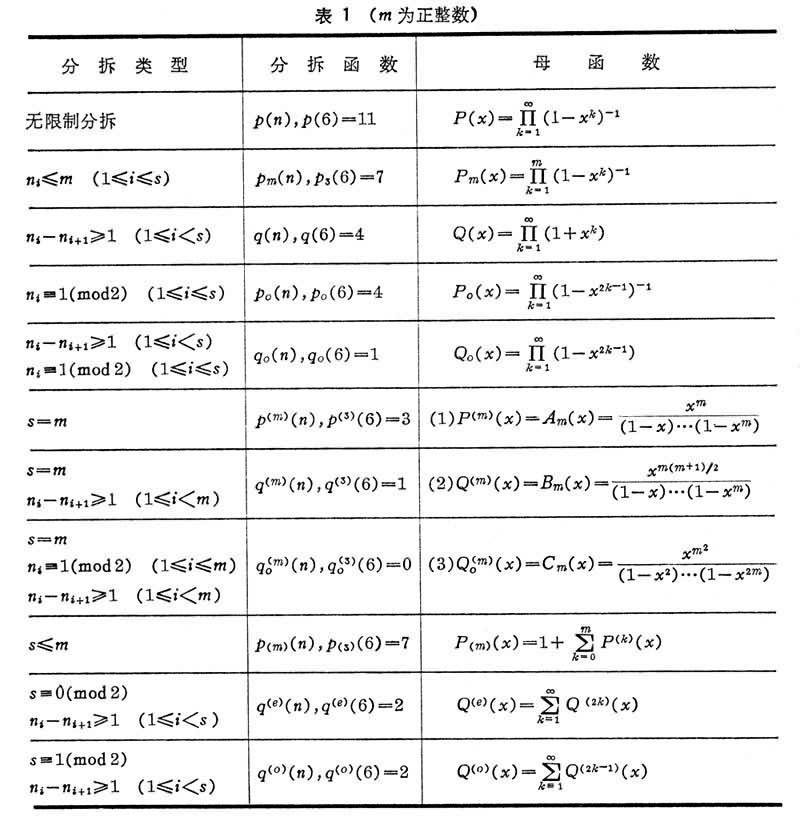
中给出了一些常见的分拆。
整数分拆理论，主要是研究各种类型的分拆函数的性质及其相互关系。早在中世纪，就有关于特殊的整数分拆问题的研究。18世纪40年代，L.欧拉提出了用母函数法（或称形式幂级数法）研究整数分拆，证明了不少有重要意义的定理，为整数分拆奠定了理论基础。解析数论中的圆法的引进，使整数分拆理论得到了进一步发展。整数分拆与模函数有密切关系，并在组合数学、群论、概率论、数理统计学及质点物理学等方面都有重要应用。
分拆函数关系式幂级数
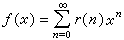称为分拆函数r(n)的母函数。在许多情形，它是容易求得的(表1)。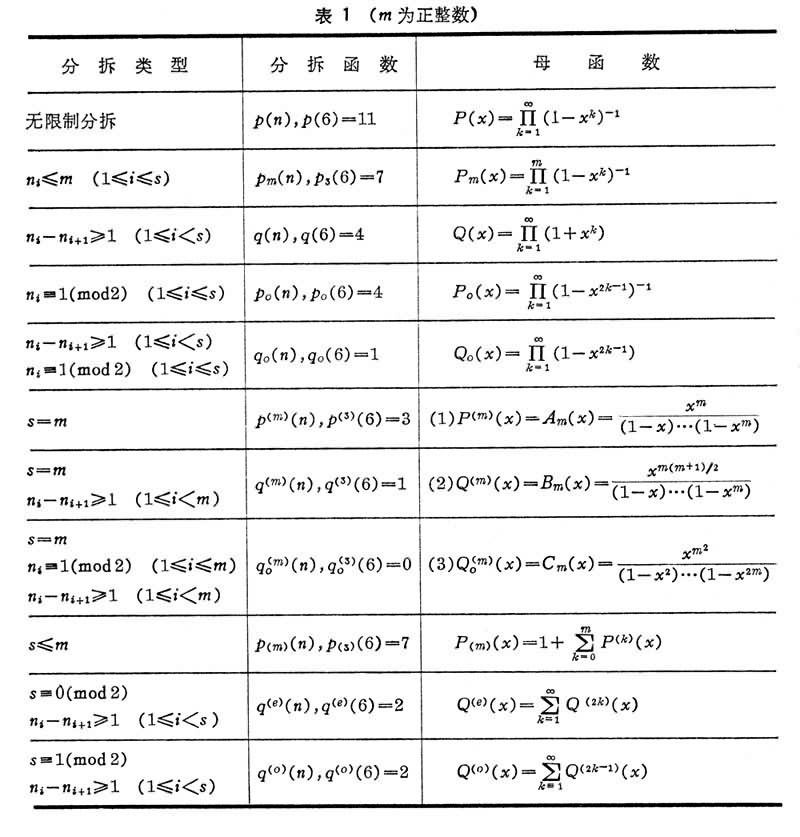
欧拉的母函数法，就是利用它来研究r(n)。从母函数之间的恒等式，可导出不同类型的分拆函数之间的关系式。如表2，其中最后一个关系式即著名的欧拉五角数定理，由此，欧拉得到了无限制分拆函数p(n)的递推公式:
，其中k取整数，ω(k)=(3k2-k)/2是五角数。利用这一公式，P.A.麦克马洪于1918年编造了p(n)(n≤200)的表。H.古普塔分别于1935年、1937年和1958年将p(n)的表扩大，直到n≤1000。
1853年，N.M.费勒斯首先提出用图示法研究分拆函数。为确定起见，分拆的被加项按不增次序排列n1≥n2≥…≥ns>0。他把n的一个分拆n=n1+n2+…+ns，用图形表示:自上而下画出s行等距圆点，第i行的圆点数为nj(1≤i≤s)，且每行左起第一个圆点位于同一列上。这种图通常称为费勒斯图。例如，16=8+4+3+1可用
表示。
利用图形的组合性质可得到不同类型的分拆函数之间的关系式，以及一些恒等式。例如，F.弗兰克林于1881年用这种方法证明了五角数定理。可以根据不同的分拆类型和问题来选用其他更合适的图形表示。分拆图示法是一个灵活而有效的方法。
与模函数的关系无限制分拆的母函数
·
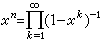是单位圆|x|<1内的解析函数。令
。得
，其中
，称为戴德金η 函数。从五角数定理可推出函数的变换公式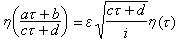
，其中α、b、с、d为满足αd-bс=1的整数，ε为一和α，b，с，d有关的24次单位根。反之，由η函数的这一变换公式可推出p(x)的一个变换公式，它在p(n)的渐近公式推导中有重要作用。此外，从模函数论中的雅可比恒等式
可推出五角数定理。
无限制分拆函数p(n)的值，随n的增长而急剧增长：
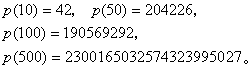
G.H.哈代和S.A.拉马努金于1918年证明估计式
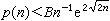，A、B为某两个正常数。他们首先提出了圆法，用它证明了渐近公式
，其中
。H.拉德马赫尔于1937年得到级数表达式
，其中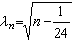
，Ak(n)是某一指数和。
S.A.拉马努金于1919年得到了p(5n+4)呏0(тod 5)，p(7n+5)呏0(тod 7)，p（11n+6）呏0(тod 11)。他还提出了一个猜想，后来发现有错，经过修正，G.W.沃森于1938年、J.勒纳于1943年与 A.D.L.阿特金于1967年证明了：若
，则
。 对其他模的同余式也有讨论。 整数分拆问题已被推广到代数数域上。此外，还可以讨论高维分拆
，r为给定正整数，以及多重分拆：
，k为给定正整数。