[拼音]：xiangliang kongjian
[外文]：vector space
又称线性空间。在解析几何学里引入向量概念后，使许多问题的处理变得更为简洁和清晰，在此基础上的进一步抽象化，形成了与域相联系的向量空间概念。向量空间是线性代数的中心内容和基本概念之一。它的理论和方法在科学技术的各个领域都有广泛的应用。
设V是一个非空集合，F是一个域。在V的元素之间定义了所谓加法，即对于V 的任意一对元素u、v，V 中有惟一确定的元素与之对应，这个元素称为u与v的和，记作u+v。在F 的元素与V的元素之间定义了所谓乘法，即对于F的任意元素α与V的任意元素u，V中有惟一确定的元素与之对应，这个元素称为α与u的积，记作αu。如果所述的加法和乘法满足以下规则，那么集合V称为域F上一个向量空间。
加法的四条规则①结合律，即u+(v+w)=(u+v)+w；
（2）交换律，即u+v=v+u；
（3）在V中存在一个“零元素”，记作0，对于V的任意元素u都有0+u=u；
（4）对于V的每一个元素u，在V中存在负元素－u，使得(-u)+u=0。
乘法的两条规则 ⑤结合律，即(αb)u=α(bu)；
（6）u是V中的任意元素，1是F的单位元素，1u=u。
加法和乘法的两条规则 ⑦α(u+v)=αu+αv；
（8）(α+b)u=αu+bu，以上各式中的u、v、w 是V的任意元素，α、b是F的任意元素。
域F上向量空间V 的元素，称为向量。V中的零元素，称为零向量。V的元素u的负元素-u，称为u的负向量。域F中的元素，称为纯量。
向量空间的加法和乘法表达出向量之间的基本关系。随着所考虑的对象不同，这两种运算的定义也不同。例如，令R是实数域，R3是一切三元实数组所成的集合，即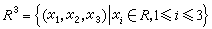
，加法的定义是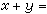 
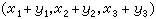，乘法的定义是
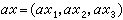，这里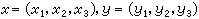
都是R3中元素，α是R中元素。于是R3是实数域上一个向量空间。设F是一个域，n是任意取定的一个正整数，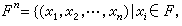
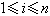定义加法为x+y=(x1+y1，x2+y2，…，xn+yn)，定义乘法为αx＝(αx1，αx2，…，αxn)，这里x＝(x1，x2，…，xn)，y＝(y1，y2，…，yn)都是Fn中元素，α是F的元素，则Fn是域F上一个向量空间。Fn是R 3的推广。在某一闭区间上连续的实函数全体所成的集合，对于函数的加法和实数与函数的乘法，是实数域上一个向量空间。次数不超过某一给定的非负整数 n的复系数多项式的全体与零多项式所成的集合p，对于多项式的加法和复数与多项式的乘法，是复数域上一个向量空间。
如果域F上一个向量空间V的非空子集W，对V的加法和乘法也构成F上一个向量空间，那么W 称为V的一个线性子空间，简称子空间。如果V的任一向量v可惟一的表为其子空间Wi的向量ui(i=1，2，…，n)的和，即v =u1+u2+…+un，那么V称为其子空间W1，W2，…，Wn的直和，记为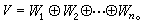
V的一个非空子集是V的子空间的充分必要条件为：对于V的任意向量u、v以及F的任意纯量α、b，有αu+bv在W中。例如，向量空间V本身以及由一个零向量所成的集合{0}，都是V的子空间，称为V的平凡子空间。向量空间Fn的子集W＝{(x1，…，xn-1，0)|xj∈F，1≤i≤n-1}，是Fn的一个子空间。系数在域F中的n元齐次线性方程组的所有的解，是Fn的一个子空间，并称为所给齐次线性方程组的解空间。
设u1，u2，…，un是域F上一个向量空间V的向量，α1，α2，…，αn是域F的元素。表示式α1u1+α2u2+ … +αnun，称为u1， u2，…，un的线性组合。如果存在F中不全为零的元素α1，α2，…，αn，使得线性组合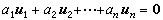
，那么u1，u2，…，un称为线性相关。在相反情形，即α1u1＋α2u2＋…＋αnun仅当
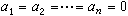时才等于零向量，则称u1，u2，…，un线性无关。如果向量空间V的向量组u1，u2，…，un满足条件：
（1）u1，u2，…，un线性无关；
（2）V的每一个向量都可以表为u1，u2，…，un的线性组合，那么向量组u1，u2，…，un称为V在F上的一个基，简称V的一个基。设尣是V的任意一个向量，u1，u2，…，un是V的一个基，于是由基的定义可知，尣=x1u1+ x2u2+…+xnun，其中x1，x2，xn是F的元素，称为向量x关于基u1，u2，…，un的坐标。对于取定的一个基，V中向量尣的坐标是惟一确定的。
一个向量空间如果有基，那么不一定只有一个基，但是 V的任意两个基所含向量的个数是相同的。一个向量空间V的基所含向量的个数，称为V的维数。只含一个零向量的向量空间的维数，约定为零。如果对于每一个自然数n，V中都存在n个线性无关的向量，那么V称为无限维的。例如，向量空间R3是三维的，e1=(1，0，0)，e2=(0，1，0)，e3=(0，0，1)是R3的一个基。向量空间Fn是n维的;连续函数构成的向量空间是无限维的；向量空间p是n+1维的。
向量空间的同构域F上两个向量空间V和V┡，如果存在V到V┡的一个双射φ:V→V┡，且满足条件φ(αu+bv)＝αφ(u)+bφ(v)，其中α、b是F中元素，u、v是V中元素，那么向量空间V和V┡称为同构的。域F上每一n维向量空间都与向量空间Fn同构。