[拼音]：erxiang fenbu
[外文]：binomial distribution
概率论中最常用的一种离散型概率分布。若随机变量X取整数值k的概率为
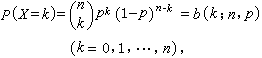
式中n是给定的正整数；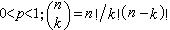
是从n个对象中任意选取k个的组合数，则称X 的分布为二项分布，记作B（n，p）。它的命名来源于b(k；n，p)恰好是[(1-p)+p]n的二项式展开的第k+1项。
从不合格品率为p的产品中独立地抽出n个（每次抽一个，抽出后又放回），其中恰有k个不合格品的概率就是b(k;n，p)；统计学由此建立检验产品质量的方案。类似的例子在生产实践和科学试验中是常见的。将这类问题模型化，假设每一次试验只有两个可能结果：A以及它的对立事件Ac，出现A的概率为P(A)=p，出现Ac的概率则为 1-p。这种只有两个可能结果的随机试验称为伯努利试验，将这种试验独立地重复进行n次所组成的随机试验称为n重伯努利试验，其中A出现的次数X是一个服从二项分布B(n，p)的随机变量。
若随机变量服从二项分布B(n，p)，则它的数学期望为np，方差为np(1-p)，特征函数为(1-p+peit)n，母函数为(1-p+ps)n。当k由0依次增大到n时，b(k;n，p)先增大后减小，当k=[(n+1)p]（记号[α]表示不超过实数α的最大整数）时，b(k;n，p)取最大值；若(n+1)p是整数，则k在(n+1)p-1及(n+1)p 处都使b(k;n，p)取最大值(见图
)。
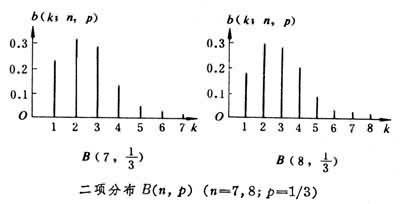
如果Xi服从B(ni，p)，i=1，2，…n，而且X1，X2，…，Xn独立，则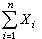
服从
。如果Xn服从B(n，p)，则对任何实数α<b，当n→∞时，有
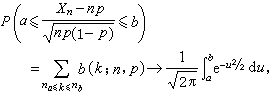
式中
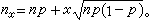
这说明，若p固定，当n充分大时，B(n，p)近似于正态分布。这个渐近公式最早由A.棣莫弗就p =1/2的情形加以证明，而后由P.-S.拉普拉斯加以推广，常称为棣莫弗－拉普拉斯中心极限定理。S.-D.泊松又证明了：若则
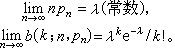
这说明，当p很小而n较大时，B(n，p)可以用泊松分布近似。
正是这两个定理揭示了概率论中最重要的正态分布和泊松分布的意义，对概率论的发展有着深远的影响。
此外，多重伯努利试验中在出现第r个A以前A不出现的试验次数的概率分布就是负二项分布，又称帕斯卡分布。特别当r=1时，就是几何分布。如果每次试验的可能结果多于两个，则二项分布就推广为多项分布。