[拼音]：biaoxiang lilun
[外文]：representation theory
研究量子力学规律的各种表示形式以及这些不同形式之间的变换的理论。微观粒子体系的状态（量子态）和力学量的具体表示形式称为表象。 微观粒子有波动和粒子两重性质，1926年E.薛定谔从粒子的波动性出发，用波动方程来描述粒子体系的运动规律，解决了许多理论和实际的问题，这种理论就是波动力学。1925年左右，由W.K.海森伯、M.玻恩、W.泡利等从粒子的粒子性出发，用矩阵的形式来描述粒子体系的运动规律，也解决了同样的问题，这种不同于波动方程的矩阵运算形式的理论称为矩阵力学。
矩阵力学和波动力学描述客观规律的形式虽然不同，但是两者实质上是一致的，它们都是描述同一微观粒子运动规律的理论。
比较直观一点，粒子体系的状态可用位置坐标为自变量、时间为参量的波函数ψ(x，t)来描述（以下均考虑一维情况，所得结果易于推广至三维），|ψ(x，t)|2表示t时刻粒子在位置坐标x附近单位体积出现的几率。但是ψ(x，t)可以用动量孨的本征函数的正交、归一、完全集{ψp(x)}展开，即
， (1)
式中
，
展开系数
(2)
可见，粒子体系的状态既可以由已知的 ψ(x，t)来描述，也可以用с(p， t)来描述。ψ(x，t)和с(p， t)是两种等价的不同表示形式的波函数。ψ (x，t)叫做坐标表象（或称x表象）波函数，с(p，t)叫做动量表象（或称p表象）波函数。
相似地ψ(x，t)可以用任一力学量孶的本征函数完全集{Un(x)}(n=1，2，3，…)展开（为了便于说明，设孶的本征值具有分立谱），即
(3)
展开系数为
(4)
因此，若已知ψ(x，t)，则同样可以通过式(4)算出an(t)来，用数字集合{an(t)}来描述这个状态，{an(t)}叫做Q表象波函数。
可见，对于同一状态，有不同的表示形式，分别都是用一组数字集合（分立的或连续的或兼而有之）来描述状态，这些不同的表示形式中的每一个叫做一个表象。当要解决某特定问题时，便选取一个特定的Q表象，相当于选取一个特定的坐标系。Q表象中的本征函数正交、归一、完全集{Un(x)}，是这一表象中的一组基矢(简称基)，它相当于坐标系中的一组单位矢量，而波函数{an(t)}是态矢量ψ 在 Q表象中各基矢方向上的投影(一组数字)，这就是表象理论的几何图像。
表示力学量的算符，在不同表象中也有不同的表示形式。 在坐标表象中， 各种力学量的算符形式是
，
是动量算符。算符
作用在波函数ψ(x，t)上得到另一个新的波函数 Ф(x，t)，即
。 (5)
在Q表象中可将ψ(x，t)和Ф(x，t)分别用孶 的本征函数完全集{Un(x)}展开，展开系数的数字集合{an(t)}和{bn(t)}就是Q表象中分别与ψ(x，t)和Ф(x，t)等价的波函数。利用{Un(x)}正交、归一的性质，可得到
(6)
式中
(7)
Q表象中的式(6)和坐标表象中的式(5)相当，写成矩阵运算形式时为
即在Q表象中， 算符弲 的表示形式是把数字集合{Fmn}排成一个方形矩阵，Fmn表示方形矩阵中第n行第m列的元素，即
而波函数ψ(x，t)和Ф(x，t)在Q表象中的表示形式，是把数字集合{an(t)}和{bn(t)}分别排成一个列矩阵，即
对于孶的本征值具有连续谱的情况，以上的论述仍然成立，只是{Un(t)}、{an(t)}和{bn(t)}等的角注 n要换成连续变化的λ，求和要换成对λ求积分，此时式 (7)写成
。
仍然把它看作矩阵元， {Fλ'λ}看成方形矩阵，{aλ(t)}和{bλ (t)}看成列矩阵，矩阵的行和列都是连续编号的。
量子力学中采用不同的表象在理论上是完全等价的，而在实际工作中选取什么表象取决于所讨论的问题，表象选得适当可以使问题简化。
可以用表象理论的几何图像来说明表象变换。选取一个特定的表象，相当于在抽象的希耳伯特空间中选取一个有一组完全基矢(本征函数集)的特定的坐标系，表象变换相当于坐标系的基矢变换，从一个A表象变换到一个B表象，相当于由一组基矢{ψn(x)}（┭的本征函数集）变到另一组基矢{嗞α(x)}（峺)的本征函数集），这种变换是通过一个变换矩阵
的作用来实现的。{ψn(x)}是完全集，B表象中的每一基矢嗞α(x)都可按{ψn(x)}展开
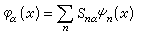， (8)
展开系数为
它是B表象中基矢嗞α(x)在A表象中基矢 ψn(x)方向上的投影，Sna就是变换矩阵s的矩阵元。
根据本征函数正交、归一的性质，容易证明
，
故得
。
式中S+是S的伴随矩阵，
-1是的逆矩阵。可见这个变换矩阵是一种幺正矩阵，式(8)中两种表象之间基矢的变换是一个幺正变换。