[拼音]：yachun hanshu
[外文]：meromorphic function
在域 G内除了极点之外为全纯的函数称为亚纯函数。一般讨论整个复平面C和扩充的复平面╦=C∪{∞}的情形。任一有理函数是整个扩充的复平面╦上的亚纯函数，它能表为两个多项式的商，并且只有有限多个极点；反之，任一在 ╦上亚纯的函数一定是一有理函数。两个无公共零点的整函数 g(z)和 g1(z)之商 g(z)/g1(z)是C上的亚纯函数，它的极点位置和重数与 g1(z)的零点相同，例如，tanz=sinz/cosz 为一亚纯函数。反之，若以亚纯函数ƒ(z)的极点作外尔斯特拉斯典型乘积g1(z)，则
ƒ(z)·g1(z)=g(z)
是一整函数，于是ƒ(z)= g (z)/ g1(z)，即每一亚纯函数能表为两个无公共零点的整函数之商。
米塔-列夫勒定理瑞典数学家G.米塔-列夫勒将有理函数部分分式表示定理推广于一般亚纯函数。每一有理函数能表为部分分式，它将函数的极点和相应的主要部分明显地指示出来。如设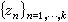
是有理函数ƒ(z)的极点，其主要部分为
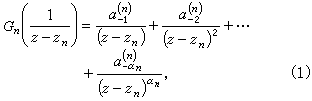
则有一适当的多项式p(z)，使得
反之，总可以构造一有理函数使得它具有预先给定的极点和主要部分。对于一般的亚纯函数自然地提出相应的问题，即是否有一个相应的“部分分式”表示，能否和如何构造一亚纯函数使得它具有预先给定的极点和相应的主要部分，以及这样的函数确定到何种程度。后一问题能立即得到回答，即任两个具有相同极点和主要部分的亚纯函数之差为一整函数。但一般亚纯函数具有无穷多个极点，而相应的主要部分之和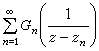
不一定收敛，因而必须修改这个级数使它收敛而同时又不引进新的奇点，这可以象整函数分解为无穷乘积一样，对上述级数的每一项加上一个适当的多项式 Pn(z)使得满足
(2)
来实现，由此得到下面以发现者命名的定理。
米塔－列夫勒定理 若给定趋于无穷的点列{zn}和相应的形如(1)的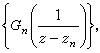
则必存在一亚纯函数
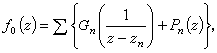
恰以{zn}为极点并以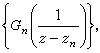
为其主要部分，其中pn(z)选取为使(2)成立的多项式。
于是具有相同极点和主要部分的最一般的亚纯函数为
ƒ(z)=ƒ0(z) +g(z) (3)
式中g(z)为任一整函数。此外，若以任一亚纯函数ƒ(z)的极点和其主要部分构造一亚纯函数ƒ0(z)，则加上适当的整函数g(z)即得ƒ(z)。换言之，任一亚纯函数能表为部分分式。这就完全解决了上面提出的问题。例如，
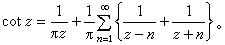柯西方法
根据上述定理得到的亚纯函数表示式中pn(z)不是惟一确定的，在应用此定理于实际例子时，主要的困难是确定(3)中的整函数g(z)。由于这个原因，柯西曾给出一种分解方法，对相当广一类亚纯函数得到简单的表示式。
令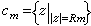 
为一圆，它不通过任何极点且包含z1，z2，…，zn为其内，又设zn≠0，首先可得
求和是对сm内之极点而作，进一步计算上式积分可得
式中k为某一正整数，pn(z)是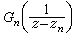
在零点邻域幂级数展式的首k项之和。假设存在一列сm，其半径Rm随m而趋向无穷，且在其上函数满足
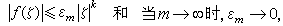
这时(4)式就是柯西给出的亚纯函数部分分式表示。