[拼音]：lianxumo
[外文]：modulus of continuity
刻画函数的连续性的一种尺度。假设ƒ(x)是定义在闭区间[α，b]上的连续函数，称
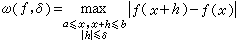
为ƒ的连续模。ω(ƒ，δ)是在 [0，l]上有定义的函数(l=b-α)，并且有如下性质：
（1）当 δ→0时，ω(ƒ，δ)→0；
（2）ω(ƒ，δ)是非负增函数；
（3）ω(ƒ，δ)是半可加的，也即对于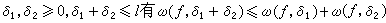
；
（4）ω(ƒ，δ)是δ的连续函数；
（5）对于自然数n， 当0≤nδ≤l时，有ω(ƒ，nδ)≤nω（ƒ，δ），对于非整数λ>0，当0≤λδ≤l时，有ω(ƒ，λδ)≤(λ+1)ω(ƒ，δ)。将ω(ƒ，δ)看作连续函数空间上的泛函，则它具有半范数的性质，也即满足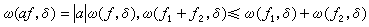
。连续模不可能太小， 对于δ→0，若
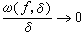，则ƒ是个常数，从而ω(ƒ，δ)恒等于零。
连续模的性质①②和③是本质的，倘若定义在[0，l]上的函数ω(δ)满足这三个性质，则它必然是[α，b]上的某个连续函数的连续模。故常称具有性质①②和③的函数为连续模函数。
如果对于任意的x，y∈[α，b]和α≥0，β≥0，α+β=1，函数g(x)满足不等式α(g(x)+βg(y)≤g(αx+βy)，则称g在[α，b]上是凹(上凸)的。如果在[0，l]上满足ω(0)=0的连续的增函数 ω(x)是凹（上凸）的，则它必然是连续模函数。当然，连续模未必是凹的，但是，对于每个连续模函数 ω(x)(0≤x≤l)，都存在凹的连续模函数ω1(x)使得
ω(x)≤ω1(x)≤2ω(x) (0≤x≤l)。
作为连续模的直接推广是光滑模。设r是自然数，对于[α，b]上的连续函数ƒ(x)，称
为ƒ的r阶光滑模，其主要性质是，对于λ>0，有
。
若ƒ有r阶连续导数，则
式中сr与с是与ƒ及δ无关的正数。