凸分析

[拼音]：tufenxi

[外文]：convex analysis

研究凸性的一门学科。它主要由凸集、（凸）多包形和凸函数三部分所组成。所谓凸集，是指一个集A，当x1和x2属于A则连接x1与x2的线段也属于A。若A是有限多个点x1，x2，…，xk+1的凸包，即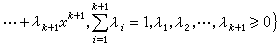，则此凸集称为一(凸)多包形。若(x1，x2，…，xk+1)的维数为k，则此多包形称为k维单纯形。若A为有限多个半闭空间的交，即A＝，则称A为一多面集。一个函数ƒ(x)称为在凸集A上的凸函数，意即当x1和x2属于A时，不等式 对所有的0 ≤λ≤1都成立。若对所有x1∈A、x2∈A和λ∈[0，1]，上述不等式以严格不等号“<”成立，则称ƒ(x)在A上为严格凸的。若将上述不等式的“≤”改为“≥”，则称ƒ(x)为A上的凹函数，相应的有严格凹函数。由于当ƒ(λ)为凹时，－ƒ(x)即为凸的，故凹函数不作为单独研究的对象。

凸集理论主要包括：分离定理，即两个无公共内点的凸集必可为一平面分开；支撑定理，即过一凸集A的一边界点，必可作一平面使A全位于此平面之一侧；一凸集到另一凸集的连续映射的性质，例如布劳威尔不动点定理等。此外，关于各种锥的性质、若干个凸集作成的集合的组合性质等也是其研究的课题。

多包形理论主要是研究多包形的代数性质、组合性质和度量性质。代数性质是指有关多包形的维数、基、代数表达式等的情况;组合性质则指有关其顶点数ƒ0，边数ƒ1，面数ƒ2，…，ƒk（ƒi表示i维面的数目）之间的关系。例如在三维空间中的欧拉定理(ƒ0－ƒ1+ƒ2＝2)即为一例。其基本问题之一是：什么样的k+1个正整数ƒ0，ƒ1，…，ƒk分别是一个k+1维多包形的顶点数、边数和面数？

凸函数理论主要包括有关凸函数的微分性质（导数、次梯度、次微分）和凸函数列的极限函数(若其存在)的性质，以及对偶性质等等。

虽然某些有关凸性的结果可追溯到18世纪中叶，但是近代的凸分析则在20世纪由H.闵科夫斯基、C.卡拉西奥多里等人创始的。他们对于多包形作了深入的研究，奠定了有关的基本理论。在20世纪中叶，由于最优化理论的发展，许多的基本理论问题皆涉及到凸性，使凸分析日益受到重视而深入发展。凸性、次梯度等在离散数学方面也受到注意。

参考书目
  1. A.Brondsted，An Introduction to Convex Polytopes，Springer-Verlag， New York， 1983.
  2. R.T.Rockafellar，Convex Analysis，Princeton Univ.Press， Princeton， 1970.
阅读全文