[拼音]：yizhi fenbu
[外文]：uniform distribution
研究实数的分数部分在区间U1=[0，1)中的分布问题。一致分布理论的发展则开始于H.外尔1916年关于一致分布理论的著名研究。一致分布除自身的发展外，在解析数论、概率论和近似分析中都有重要的应用。例如，关于外尔和估计的研究是解析数论与堆垒数论中的核心。
命xj(i=1，2，…)为U1中的一个点集。对于任意正整数n及任意实数r∈U1，命Nn(r)表示n个点xj(1≤i≤n)落入区间[0， r)的点的个数。如果
，
则称点集xj(i=1，2，…)在U1中一致分布。
外尔给出了判断一致分布的重要法则，即所谓外尔判别法:点集xj(i=1，2，…)在U1中一致分布的充分必要条件为，对于任一U1中的黎曼可积函数ƒ(x)，皆有
。
应用这一法则十分困难，因为需对所有黎曼可积函数进行研究才能证明点集的一致分布性，于是导致外尔在黎曼可积函数的集合中，选出一个特殊的序列
，
其线性包给出每一黎曼可积函数。从而他证明了下面更精密的判别法：数列xj(i=1，2，…)在U1中一致分布的充分必要条件为，对于任意整数h≠0，常有
。
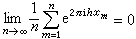例如，对于任何实无理数α，数列nα( n=1，2，…)对模1是一致分布，即它们的分数部分｛nα｝(n=1，2，…)在U1中一致分布。又如，若多项式ƒ(x)的次数大于或等于1，其系数为实数且至少有一个系数为无理数，则数列ƒ(x)(x=1，2，…)对模1是一致分布。
命
，
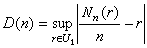D(n)称为点列xj(1≤i≤n)的偏差。因此，若点集xj(i=1，2，…)在U1中一致分布，则
或D(n)=O(1)。偏差是用来刻画一致分布点集的分布误差的。关于偏差的重要结果如下：
对于U1中任意n个数xj(1≤i≤n)及任意正整数m皆有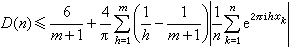
。这基本上是P.爱尔特希和P.图兰得到的。
对于U1中任意n个点皆有
，此处с为一个正的绝对常数。这是K.F.罗特得到的。
一致分布的定义可以推广到s维欧几里得空间，此处s≥2。命Us表示s维单位立方体，即适合0≤xj≤1，1≤i≤s的全体点尣 =(x1，x2，…，xs)。命p(h)=(x1(h)，x2(h)，…， xs(h))(h=1，2，…)为Us中的点集。对于任意r=(r1，r2，…，rs)∈Us，命Nn(r)表示适合下面条件的p(h)(1≤h≤n)的个数0≤xj(h)< rj，1≤i≤s，则这n个点的偏差定义为
，
此处|r|=r1r2…rs。若D(n)=O(1)，则称点集p(h)(h=1，2，…)在Us中一致分布。
外尔判别法及关于偏差的结果，在s维空间都有相应的推广。
一致分布的定义及外尔判别法还可以推广到紧致空间与拓扑群。
一致分布理论中有不少待解决的问题。例如数列ex(x=1，2，…)是否对模1为一致分布，就是未解决的著名问题。