[拼音]：xiangliang fenxi
[外文]：vector analysis
与向量函数有关的微积分运算及其应用。
向量函数的微分法设有一依赖于某变量 t的向量函数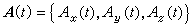
（t在某一区间α≤t≤β上变化）。如果下面这极限存在，则称
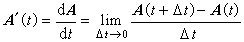
为A(t)在t处的导数。导数存在的充分必要条件是三个分量函数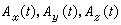
在t处都有导数，且恒有
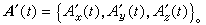
也可定义向量函数的微分：
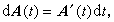
或即
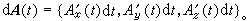
类似地可定义向量函数的高阶导数与高阶微分。
如向量函数依赖于多个自变量，例如A(u，v)，则也可定义偏导数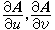
以及全微分
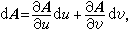
等等。
向量函数的积分法A(t)在区间[α，β]上的积分定义为
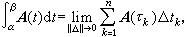
式中Δ为[α，β]的一分划：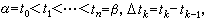
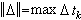，而τk为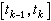
中任何一点。用分量写法，则有 
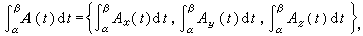当然要假定各分量的积分存在。
也可以定义重积分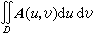
以及线积分、面积分等等。
总之，向量函数的微分法与积分法都可通过它的各分量的相应运算来实现。
设A(t)为一曲线C上动点的位置向量，t为流动参数，亦即，C有参数方程
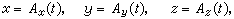
则A┡(t)的方向就和曲线C在t处的切线方向相同。如果A(u，v)是一曲面S上动点的位置向量，而u，v为流动参数，则向量积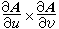
的方向就和曲面S上(u，v)处的法线方向相同。用这些基本事实，可以来研究空间曲线、曲面的性质，也是微分几何的出发点。