[拼音]：Meisenshu
[外文]：Mersenne numbers
形如2p-1的数，记为Mp，这里p 是素数。1644年，M.梅森证明了当p=2，3，5，7，13，17，19，31时，Mp是素数。到目前为止，只知道28个梅森数是素数，除已提到的8个以外，另外20个是Mp=2p-1，p=61，89，107，127，521，607，1279，2203，2281，3217，4253，4423，9689，9941，11213，19937，21701，23209，44497，86243，其中2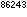
-1是所知道的最大素数，长达25962位。
关于梅森数有一些简单性质：
（1）设p是奇素数，素数q｜Mp，则q形如q=2kp+1。
（2）设p=4n+3是一个素数，则2p+1=8n+7是一个素数的充分必要条件是2p+1|Mp。由此推出，23｜M11，47｜M23，167｜M83，263｜M131，359｜M179，383|M191，479｜M239，503｜M251等。
（3）设p≠q，则(Mp，Mq)=M(p，q)=1。
19世纪，E.拉库斯给出了一个判断Mp是否为素数的方法：若有墹>0使
，且在二次域
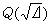中有一个单位数ε适合N(ε)=-1，则Mp为素数的充分必要条件是
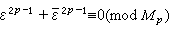，式中
为ε的共轭数。1930年，D.H.莱默尔改进了E.拉库斯的结果，得到判别法则：设p是一个奇素数，定义序列
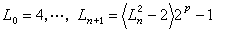(n≥0)，
则2p-1是素数当且仅当lp-2=0。对于大的Mp，一般都用这个方法在计算机上进行计算来判断它是否为素数。梅森数与偶完全数密切相关，求偶完全数等价于求梅森数中的素数。是否有无穷多个p使Mp为素数，是数论中尚未解决的著名问题。还有一个未曾解决的猜想是:Mp无平方因子。1967年，L.J.沃伦证明了若素数q满足q2|Mp，则
。
梅森数在诸如代数编码的一些应用学科中有用。