[拼音]:dianci guilü de xiebian xingshi
[外文]:covariant form of electromagnetic law
狭义相对论指出,对于一切惯性参照系,物理规律都是相同的,而且不同惯性系之间的变换关系是洛伦兹变换。因此,所有描述基本物理规律的方程式,都应该在洛伦兹变换下保持不变。这种不变性就称为洛伦兹不变性。
为了显示一个或一组物理方程的洛伦兹不变性,通常将它表示成这样的形式,使得方程中各项在洛伦兹变换下都具有确定的,并且彼此相同的变换性质。这样,当从一个惯性参照系变换到另一个惯性参照系时,就能得到相同的方程式。具有上述形式的方程就称为协变形式的方程。
电磁量的洛伦兹变换洛伦兹变换是一个四维变换,因此在洛伦兹变换下的矢量常称为四维矢量或简记作4-矢量。例如三维空间的坐标(x1,x2,x3)配上时刻t就合成一个4-矢量(x0,x1,x2,x3),其中x0=сt,с为真空中光速。此矢量称为四维时空坐标xμ(μ=0,1,2,3)。在电磁量(本条采用高斯单位制)中,通常的三维电流密度(j1,j2,j3)同电荷密度 ρ 配成一个四维矢量(j0,j1,j2,j3),其中j0=ρс。这个矢量就称为四维电流密度 jμ。洛伦兹规范下的电磁矢量势(A1,A2,A3)和标量势嗞也配成一个 4-矢量(A0,A1,A2,A3),其中A0=嗞,称为四维电磁势Aμ。当两个惯性参照系s和s′的空间坐标轴取得彼此平行而且s′沿x轴方向以速度v相对s运动时(并取t=t′=0为两参照系坐标原点相重合的时刻)两者时空坐标间的变换关系为:
 (1)
(1)
此即时空坐标的洛伦兹变换。根据矢量的变换性质,s和s┡中电流密度和电磁势也具有类似的变换关系:
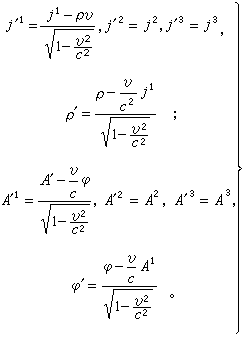 (2)
(2)
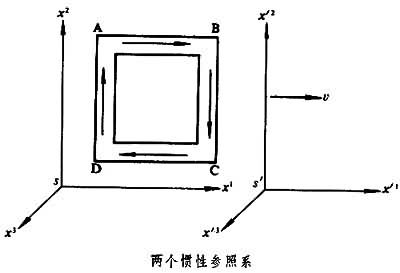
由此可以得出,如果在s参照系中有一静止的均匀导体回路,其内j1 0而ρ=0,则在s′参照系中将观测到ρ′
0而ρ=0,则在s′参照系中将观测到ρ′ 0(见图)。如从s′参照系观测,图中AB段就将带负电,而CD段将带正电。上述电荷的出现可用洛伦兹收缩来说明。与此相应,在s参照系中嗞=0,只有A;而在s′参照系中嗞 ┡和A′都将不为零。
0(见图)。如从s′参照系观测,图中AB段就将带负电,而CD段将带正电。上述电荷的出现可用洛伦兹收缩来说明。与此相应,在s参照系中嗞=0,只有A;而在s′参照系中嗞 ┡和A′都将不为零。
在洛伦兹变换下,电场强度E和磁感应强度B合起来按一个二阶张量来变换,此张量用矩阵表示为:
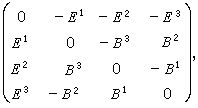
它的分量记作Fμv(μ、v从0到3),并称为电磁场场强张量。在上述两个惯性参照系s和s′中的场强值,有如下的关系:
E'1=E1, B'1=B1,
 (3)
(3)
当略去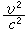 的小项时,上式可写作
的小项时,上式可写作
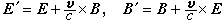 。 (4)
。 (4)
v代表在s系中所观测的s′系的速度。这样,若在s系中只有电场或只有磁场,则在s′系中将同时有电场和磁场存在。以上结果表明了电场同磁场之间深刻的内在联系,实际上它们是统一的电磁场场强张量的不同分量。
电磁场的能量密度u和能流密度(S1,S2,S3)以及动量密度(g1,g2,g3)和动量流密度φij(i,j取1到3)合起成一个二阶张量
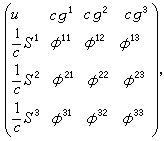
此张量称为电磁场的能量-动量张量,并用Tμv表示。
电磁规律的协变形式麦克斯韦方程组中的两个方程
 , (5)
, (5)
可以合起来用
 (6)
(6)
表示,其中
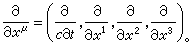
v=0代表式(5)的第一式,v=1,2,3代表式(5)的第二式。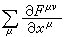 代表张量Fμυ的四维散度,它是一个四维矢量。这样式(6)左右两方都是四维矢量,符合协变要求。
代表张量Fμυ的四维散度,它是一个四维矢量。这样式(6)左右两方都是四维矢量,符合协变要求。
麦克斯韦方程组中的另外两个方程
 (7)
(7)
可以合起来用
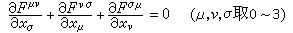 (8)
(8)
表示。注意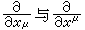 ,前者代表
,前者代表


这是因为洛沦兹变换不是正交变换,故对于矢量和张量还必须区别为逆变和共变两类。前面所说的xμ、jμ、 Aμ和这里的微分算符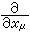 都是逆变矢量,而微分算符
都是逆变矢量,而微分算符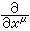 则为共变矢量。式 (8)中每一项都代表一个三阶的逆变张量,故该式是协变的。
则为共变矢量。式 (8)中每一项都代表一个三阶的逆变张量,故该式是协变的。
这里,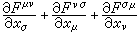 对于指标(μ,v,σ)为完全反对称的,故式(8)实际上只包含四个独立的方程,它们的(μ,v,σ)可取为(1,2,3),(2,3,0),(3,0,1)和(0,1,2)。当(μ,v,σ)取(1,2,3)时,式(8)相应于 墷·B=0,而当(μ,v,σ)取(2,3,0),(3,0,1)和(0,1,2)时,式(8)相应于
对于指标(μ,v,σ)为完全反对称的,故式(8)实际上只包含四个独立的方程,它们的(μ,v,σ)可取为(1,2,3),(2,3,0),(3,0,1)和(0,1,2)。当(μ,v,σ)取(1,2,3)时,式(8)相应于 墷·B=0,而当(μ,v,σ)取(2,3,0),(3,0,1)和(0,1,2)时,式(8)相应于
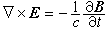 。
。
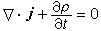 , (9)
, (9)
其协变形式为
 , (10)
, (10)
即四维电流密度的四维散度为零。而洛伦兹规范下矢量势和标量势的方程
 (11)
(11)
其协变形式即为:
 (12)
(12)
式中,
在洛伦兹变换下,三维力密度(f1,f2,f3)和功率密度w亦配成四维矢量(f0,f1,f2,f3),其中 ,并称为四维力密度,用fμ表示。这时,洛伦兹力公式:
,并称为四维力密度,用fμ表示。这时,洛伦兹力公式:
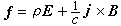 , (13)
, (13)
和功率公式
ω=E·E。 (14)
可以合起来写成
 , (15)
, (15)
其中jv表示(ρс,-j1,-j2,-j3)为一共变矢量。式(15)在μ=0时化为式(14),而在μ=1,2,3时化为式(13)。式(15)两侧都是逆变矢量,因而方程是协变的。
能量和动量守恒定律
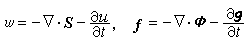 , (16)
, (16)
如前所述s为能流密度;Φ为动量流密度,系张量;g为动量密度, ,可以合起来写成下述协变形式的方程:
,可以合起来写成下述协变形式的方程:
 。 (17)
。 (17)
以上结果还显示了电磁场能量和动量之间密切的内在联系。
也可采用与以上不同的另一种数学描述,即不引入x0=сt,而引入一个虚数x4=iсt来构成四维时空矢量(x1,x2,x3,x4),在这种描述下,洛伦兹变换形式上为一个正交变换,于是就不必区分共变和逆变两类矢量和张量,从而在数学上得到了简化。