[拼音]:gongxing yingshe
[外文]:conformal mapping
又称保角映射,复变函数论的一个分支。它是从几何的观点来研究复变函数。若解析函数w=ƒ(z)在域D中单叶(见单叶函数),且将D 映为域墹 ,则在D 中的(有限)点z处,ƒ′(z)≠0,在D中任取一点z0 ,Cz为过z0的在D 内的任一简单光滑曲线:z=z(t)=x(t)+iy(t)(α≤t≤b),其中x(t)及y(t)是z(t)的实部与虚部。设z(t0)=z0(α≤t0≤b), 曲线 Cz在 z=z0的切线与实轴的夹角是 z′(t0)的幅角Argz′(t0)。w =ƒ(z)将Cz映为 墹 中过w 0=ƒ(z0)的一条简单光滑曲线Cw:w =ƒ(z(t))(α≤t≤b)。由于 Cw在w0的切线与实轴的夹角是
Cw在w0的切线与实轴的夹角是
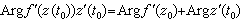 。
。
所以Cw在w0处切线与实轴的夹角同Cz在z0处的切线与实轴的夹角相差Argƒ′(z0)。这个值与曲线Cz的形状及方向无关。因此,若在D中一点z0,过z0点有D中的二条光滑曲线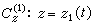 及
及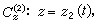 则这二条曲线在z0的交角,即这二条曲线在z0点的切线的夹角为
则这二条曲线在z0的交角,即这二条曲线在z0点的切线的夹角为 。w=ƒ(z)将C
。w=ƒ(z)将C ,C嶤分别映为墹中的二条光滑曲线C
,C嶤分别映为墹中的二条光滑曲线C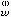 ,C
,C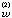 。则C
。则C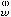 与C
与C 之间的夹角为
之间的夹角为 ·
·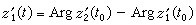 。也就是,用单叶解析函数w=ƒ(z)作映射时,曲线间的夹角的大小及方向保持不变,所以称w =ƒ(z)为保角变换或保角映射。由于
。也就是,用单叶解析函数w=ƒ(z)作映射时,曲线间的夹角的大小及方向保持不变,所以称w =ƒ(z)为保角变换或保角映射。由于 
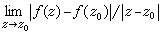 ,故当|z-z0|充分小时,|ƒ(z)-ƒ(z0)|还近似地等于|ƒ′(z0)||z-z0|,即经过w =ƒ(z), |z-z0| 近似地伸缩了|ƒ′(z0)|倍 。这个数与向量z-z0的方向无关,故称|ƒ′(z0)|为在点z0的伸缩率,于是在D 中一点z0一个领域内的任一小三角形,经w =ƒ(z)映射后,映为Δ中含w0=ƒ(z0)的一个邻域内的一个曲边三角形,这两三角形对应角相等,对应边近似地成比例,因此这两个三角形近似地是相似形。因此,称w =ƒ(z)的映射为共形映射,或保形映射,即在一点的附近,w =ƒ(z)几乎保持了几何的形状。
,故当|z-z0|充分小时,|ƒ(z)-ƒ(z0)|还近似地等于|ƒ′(z0)||z-z0|,即经过w =ƒ(z), |z-z0| 近似地伸缩了|ƒ′(z0)|倍 。这个数与向量z-z0的方向无关,故称|ƒ′(z0)|为在点z0的伸缩率,于是在D 中一点z0一个领域内的任一小三角形,经w =ƒ(z)映射后,映为Δ中含w0=ƒ(z0)的一个邻域内的一个曲边三角形,这两三角形对应角相等,对应边近似地成比例,因此这两个三角形近似地是相似形。因此,称w =ƒ(z)的映射为共形映射,或保形映射,即在一点的附近,w =ƒ(z)几乎保持了几何的形状。
共形映射有广泛的应用。应用它可以成功地解决流体力学与空气动力学,弹性理论以及场论等很多方面的许多实际问题。例如H.E.茹科夫斯基应用著名的茹科夫斯基函数 作为出发点,来研究各种飞机机翼截面,是很有成效的。
作为出发点,来研究各种飞机机翼截面,是很有成效的。
共形映射理论中最基本的定理是黎曼映射定理:至少有两个边界点的任意单连通区域一定可以共形映射到单位圆的内部。如果对域中指定一点z0要求将z0映为0,且 Argƒ′(z0)等于已给的θ0,那么这样的映射是惟一的,这是黎曼于1851年证明的,当时的证明略有不足之处,经后人补充完整,对于多连通区域也有相应的定理,但要求多连通区域的模相同。当两个多连通域的模相同时,才有亚纯函数存在,使它们相互共形映射。
将单位圆映为单位圆的共形映射为  ,这里
,这里 。所有这些映射的全体组成一个群,称为麦比乌斯变换群。 将上半平面Im z >0 映为上半平面Imw>0的映射为
。所有这些映射的全体组成一个群,称为麦比乌斯变换群。 将上半平面Im z >0 映为上半平面Imw>0的映射为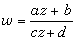 ,其中α,b,с,d为实数,αd -bс≥0,将上半平面Im z>0映为单位圆|w|<1 的映射为
,其中α,b,с,d为实数,αd -bс≥0,将上半平面Im z>0映为单位圆|w|<1 的映射为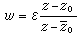 ,其中Imz0>0,|ε|=1。 另外一个有用的映射公式是施瓦兹-克里斯托费尔公式,是由 H.A.施瓦兹和E.B.克里斯托费尔于19世纪60年代开始研究的,讨论将单位圆内部到上半平面内部共形映射到多边形内部的解析函数。若P为w平面上的多边形,顶点为bμ(μ =1,2,…,m),bμ的内角为αμπ,则w =ƒ(x)将单位圆或上半平面映为P的内部的公式为
,其中Imz0>0,|ε|=1。 另外一个有用的映射公式是施瓦兹-克里斯托费尔公式,是由 H.A.施瓦兹和E.B.克里斯托费尔于19世纪60年代开始研究的,讨论将单位圆内部到上半平面内部共形映射到多边形内部的解析函数。若P为w平面上的多边形,顶点为bμ(μ =1,2,…,m),bμ的内角为αμπ,则w =ƒ(x)将单位圆或上半平面映为P的内部的公式为
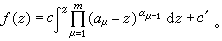
这里
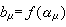 ,
,
с,с┡为依赖于P 的位置、大小的常数。对于多连通区域也有相应的施瓦兹-克里斯托费尔变换公式。
- 参考书目
- C .Carathéodory,ConforMal Representation,CambridgeUniv.Press,Cambridge,1932.
- S.Bergman,The Kernal Function and ConforMal Mapping,Amer. Math.Soc.Math.Surveys,Providence,1950.
- Z.Nehari,ConforMal Mapping,McGraw-Hill,NewYork,1952.