[拼音]：kongjian qulü
[外文]：curvature of space
表征某种给定度规的空间对于欧氏空间的偏离程度的量。举例说，球面是一种二维的弯曲空间，球面上弧元的平方是：
。
式中U、嗞 为球面上的点在过球心的平面上投影的坐标;R是球的半径;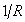
是这个空间的曲率。对于一般的二维曲面上的各个点，能借两个单参数曲线族（μ =常数，v =常数）所定义的坐标μ 和v 来表示。在其上弧元的平方是：ds2=g11dμ2+2g12dμdv+g22dv2，式中g11、g12、g22为坐标μ、v的函数。它反映着空间的度量性质。过这种曲面上的每一点作切面，在切面上存在两个互相垂直的方向。在这两个方向上曲率1/R，分别达到极大值和极小值1/R1和1/R2。量
称为高斯曲率。
黎曼研究了更一般的弯曲空间。在满足一定条件的集合中给定一个二阶协变张量场；对于局部坐标x1，…，xn，这个张量场可以写为gij(x1，…，xn)，它是对称的，并且是非退化的。这样的集合称为黎曼空间。gij称为黎曼空间的度规张量。在这种空间中的弧元平方定义为ds2=gij(x1，…，xn)dxidxj。上指标与下指标相同，代表这个指标分别取空间中各维来求和。这种空间的弯曲性质用黎曼曲率张量表示为：
式中
，
被称作联络。由Rλμvx经过一次升标和缩并运算，可以得到另外两个表征空间弯曲的量，即里齐张量Rμv和标量曲率R。由某点上两个线性独立的方向 ξ媰，ξ媱决定的标量：
叫作黎曼空间在该点的黎曼曲率。