卷积

[拼音]：juanji

[外文]：convolution

分析数学中一种重要的运算。设ƒ(x)，g(x)是R¹上的两个可积函数，作积分

。

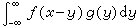可以证明，关于几乎所有的x∈(-∞，∞)，上述积分是存在的。这样，随着x的不同取值，这个积分就定义了一个新函数h(x)，称为ƒ与g的卷积，记为h(x)=(ƒ*g)(x)。容易验证，(ƒ*g)(x)=(g*ƒ)(x)，并且(ƒ*g)(x)仍为可积函数。这就是说，把卷积代替乘法，l¹(R¹)空间是一个代数，甚至是巴拿赫代数。

卷积与傅里叶变换有着密切的关系。以弮(x)，抭(x)，表示l¹(R¹)中ƒ和g的傅里叶变换，那么有如下的关系成立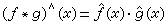：，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。这个关系，使傅里叶分析中许多问题的处理得到简化。

由卷积得到的函数(ƒ*g)(x)，一般要比ƒ，g都光滑。特别当g为具有紧支集的光滑函数，ƒ为局部可积时，它们的卷积(ƒ*g)(x)也是光滑函数。利用这一性质，对于任意的可积函数，都可以简单地构造出一列逼近于ƒ 的光滑函数列ƒ_s(x)，这种方法称为函数的光滑化或正则化。

卷积的概念可以推广到数列、测度以及广义函数上去。例如，α={α_n}，b={b_n}(n=0，±1，±2，…)为两个数列，新的数列

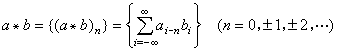
定义为数列α与b的卷积。在概率论中也遇到卷积的概念。例如，已知独立随机变量ξ和η的概率分布为P_ξ（A）和P_η(A)，那么随机变量ξ+η的分布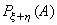由下式给出

，

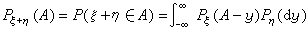式中A-y表示点集{x|x+y∈A};A为直线上任意的波莱尔集。

卷积，作为运算，还具有十分重要的所谓平移不变性。例如以τα表示平移算子，即(ταƒ)(x)=ƒ(x-α)，那么就有

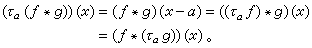
利用这性质，可以刻画出l^p(R¹)到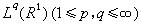有界的平移不变算子的特征，即当作用在施瓦兹函数类(记为S(R¹))时，这种算子一定是某个缓增广义函数u与函数φ∈S的卷积u*φ（见广义函数）。