[拼音]:guangyi hanshu
[外文]:generalized function,distribution
古典函数概念的推广。关于广义函数的研究构成了泛函分析中有着广泛应用的一个重要分支。历史上第一个广义函数是由物理学家 P.A.M. 狄喇克引进的,他因为陈述量子力学中某些量的关系时需要引入了“函数”δ(x):当 x≠0时,δ(x)=0,但 。按20世纪前所形成的数学概念是无法理解这样奇怪的函数的。然而物理学上一切点量,如点质量、点电荷、偶极子、瞬时打击力、瞬时源等物理量用它来描述不仅方便、物理含义清楚,而且当它被当作普通函数参加运算,如对它进行微分和傅里叶变换,将它参与微分方程求解等所得到的数学结论和物理结论是吻合的。这就迫使人们要为这类怪函数确立严格的数学基础。最初理解的方式之一是把这种怪函数设想成直线上某种分布所相应的“密度”函数。所以广义函数又称为分布,广义函数论又叫做分布理论。用分布的观念为这些怪函数建立基础虽然很直观,但对于复杂情况就又显得繁琐而不很明确。后来随着泛函分析的发展,l.施瓦尔茨(1945)用泛函分析观点为广义函数建立了一整套严格的理论,接着И.М.盖尔范德对广义函数论又作了重要发展。从此,广义函数被广泛地应用于数学、物理、力学以及分析数学的其他各个分支,例如微分方程、随机过程、流形理论等等,它还被应用到群的表示理论,特别是它有力地促进了偏微分方程近30年来的发展。
。按20世纪前所形成的数学概念是无法理解这样奇怪的函数的。然而物理学上一切点量,如点质量、点电荷、偶极子、瞬时打击力、瞬时源等物理量用它来描述不仅方便、物理含义清楚,而且当它被当作普通函数参加运算,如对它进行微分和傅里叶变换,将它参与微分方程求解等所得到的数学结论和物理结论是吻合的。这就迫使人们要为这类怪函数确立严格的数学基础。最初理解的方式之一是把这种怪函数设想成直线上某种分布所相应的“密度”函数。所以广义函数又称为分布,广义函数论又叫做分布理论。用分布的观念为这些怪函数建立基础虽然很直观,但对于复杂情况就又显得繁琐而不很明确。后来随着泛函分析的发展,l.施瓦尔茨(1945)用泛函分析观点为广义函数建立了一整套严格的理论,接着И.М.盖尔范德对广义函数论又作了重要发展。从此,广义函数被广泛地应用于数学、物理、力学以及分析数学的其他各个分支,例如微分方程、随机过程、流形理论等等,它还被应用到群的表示理论,特别是它有力地促进了偏微分方程近30年来的发展。
在广义函数理论的形成过程中有重要影响的有:j.(-s.)阿达马 (1932)在研究波动方程基本解时使用了发散积分的有限部分。С.Л.索伯列夫(1936)在研究双曲型方程的柯西问题时用分部积分引入了广义导数和微分方程广义解的概念,并把函数δ及其导数δ′等视为某个函数空间上的线性泛函;他对广义函数论的建立迈出了决定性的一步。s.博赫纳(1932)和T.卡莱曼(1944)讨论了幂增长函数的傅里叶变换,提出了连续函数的形式导数概念。
当然为那些怪函数建立严格数学基础的方法并不是惟一的,例如波兰学者J.米库辛斯基就曾用较初等的方法建立它们的基础。也有把广义函数看作解析函数的边界值,并由此发展出超函数理论。换句话说,广义函数的定义并不完全统一,而是具有一定程度的灵活性,可以根据问题的需要适当地定出相应的广义函数类。
基本函数空间和广义函数空间
泛函分析观念下的广义函数理论的核心是把广义函数看成某个函数空间上的连续线性泛函,即先选取某些性质很好的函数组成的线性空间,再在其中给出适当的收敛概念,这样的函数空间就称为基本函数空间,又称为测试函数空间,而其中每个函数称为基本函数或测试函数。相应于基个基本空间上的连续线性泛函就称为该基本空间上的广义函数。广义函数全体就称为相应于基本空间的广义函数空间。常用的基本空间有K空间和S空间。
基本函数空间K
设 φ(x)是定义在n维欧几里得空间 Rn上的复值函数,用Sφ表示集{x|φ(x)≠0}的闭包,称为φ(x)的支集。对任意n个非负整数p1,p2,…,pn。记
 ,
, ,和
,和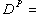

 。
。
设K是 Rn上无限次可微而且支集有界的复函数全体,K按通常函数的线性运算成为复线性空间。在K上引进极限概念如下:设{φn}嶅K, φ∈K, 如果满足①对于函数列{φn}存在有界区域Ω, 使所有函数 φn在Ω外为0,即S拻嶅Ω,②对每个 ,函数列Dp(φn-φ)一致收敛于0;则称{φn}在K中收敛于φ,记为φn
,函数列Dp(φn-φ)一致收敛于0;则称{φn}在K中收敛于φ,记为φn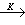 φ。赋予上述线性运算和极限运算的 K,作为基本函数空间,简称K空间;其中的每个函数称为基本函数。K空间上收敛概念的严格叙述要用到拓扑线性空间的严格归纳极限概念。
φ。赋予上述线性运算和极限运算的 K,作为基本函数空间,简称K空间;其中的每个函数称为基本函数。K空间上收敛概念的严格叙述要用到拓扑线性空间的严格归纳极限概念。
K空间上的广义函数
设 ƒ是定义在K空间上的复值函数,如果ƒ(φ)是K上连续线性泛函,即满足①(线性)对任意φ1,φ2∈K,复数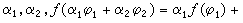
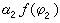 ,②(连续性)对于基本函数列φn
,②(连续性)对于基本函数列φn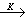 0,ƒ(φn)→0;则称ƒ为K空间上的广义函数,并把ƒ(φ)写成 <ƒ,φ>或形式地写成
0,ƒ(φn)→0;则称ƒ为K空间上的广义函数,并把ƒ(φ)写成 <ƒ,φ>或形式地写成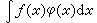 。K 空间上广义函数全体记为K′。K′按通常线性运算也是一个线性空间。
。K 空间上广义函数全体记为K′。K′按通常线性运算也是一个线性空间。
K上广义函数的例子
(1)设ƒ(x)是Rn上的可测函数,如果在每个有界闭立方体上勒贝格可积,则称为局部可积函数, 其全体记为l*。在l*中几乎处处相等的函数看作相同。对每个ƒ∈l*,令
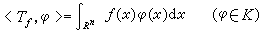 ,
,
式中dx是Rn上的勒贝格测度。上式确定的Tƒ是K上的一个广义函数。也就是说,普通的局部可积函数可以等同于K上一个广义函数,称为正则广义函数。
(2)由下式定义的泛函 ,是K上广义函数,通常形式地记δ为δ(x)。
,是K上广义函数,通常形式地记δ为δ(x)。
(3)设μ是Rn中波莱尔可测集上的复值的可列可加集函数,并且在每个紧集上测度有限,由 ·μ(dx)定义的Tμ是 K上的一个广义函数。
·μ(dx)定义的Tμ是 K上的一个广义函数。
(1),②中的广义函数都是它的特例。
(4)单变量函数 在R上不是局部可积的,令
在R上不是局部可积的,令

(PV表示柯西主值)。 是R上的一个广义函数。
是R上的一个广义函数。
K′上的拓扑
在K′上可如下引进序列收敛概念。设{Fn}嶅K′,F∈K′,如果对每个φ∈K有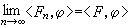 ,那么称{Fn}在K′中收敛到F,记为
,那么称{Fn}在K′中收敛到F,记为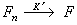 。
。
广义函数的支集
对于广义函数一般说来在某一点的值是没有意义的。例如不能讲广义函数F在x0点为0,但可以说广义函数F 在某邻域(开集)U 中为0,它的意思是,对每个支集在U 中的基本函数φ ,<F,φ >=0,记为 F|U=0。并集 ∪{U|F|U=0}的余集SF称为广义函数F的支集。一般地,例①中ƒ(x)如果是连续函数,那么它的支集和Tƒ的支集 是一致的。
是一致的。
K上广义函数的导函数和原函数
当F 是K空间上的广义函数时,显然 也是K上的广义函数,称它是广义函数F对xi的偏导数,记为
也是K上的广义函数,称它是广义函数F对xi的偏导数,记为 ,即
,即
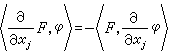 。
。
当ƒ(x)是Rn上普通的连续可微函数时,ƒ作为广义函数意义下的导数和ƒ 的经典导数是一致的。可见广义函数导数概念是普通导数概念的推广。但从广义函数导数的定义可以知道,对于每个广义函数存在任意阶的广义导函数,并且可以交换广义函数求导次序。另外广义函数的求导运算和极限运算是可以交换的。上述性质表明广义函数的出现解除了经典分析中对求导运算和对函数列的极限进行求导运算的种种限制。例如对于 R上亥维赛函数θ(x):当x≥0时,θ(x)=1。当x<0时,θ(x)=0,它的广义导数 ,而
,而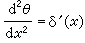 。
。
广义函数也可定义原函数或不定积分。设 F是单实变量的K 空间上广义函数,如果广义函数G满足 ,则称G为F的原函数。对于每一个广义函数F∈K′,必存在原函数G,F的一切原函数必然形如G+с,其中с是常数。
,则称G为F的原函数。对于每一个广义函数F∈K′,必存在原函数G,F的一切原函数必然形如G+с,其中с是常数。
K上广义函数的构造
利用广义函数的导数概念可以给出一类广义函数的结构。下述定理表明 K上每个广义函数局部地是一个有界函数的导函数。
K空间上广义函数的局部构造定理:设F∈K′,w是Rn中有界开集,则F在w上等于一个具有有界支集的连续函数的导函数。
特别,每一个具有有界支集的广义函数F∈K′必能表示为 ,其中ƒp都是有有界支集的连续函数,r是某个自然数。更为特别的是,如果广义函数F的支集仅有一点α,那么F能表示为
,其中ƒp都是有有界支集的连续函数,r是某个自然数。更为特别的是,如果广义函数F的支集仅有一点α,那么F能表示为 ,式中αp为数,且
,式中αp为数,且 。
。
K 上广义函数的傅里叶变换
设 
 。称F:φ
。称F:φ 愩为傅里叶变换。记愩=F(φ)。K中函数的傅里叶变换全体组成的线性空间记为Z=FK。如果
愩为傅里叶变换。记愩=F(φ)。K中函数的傅里叶变换全体组成的线性空间记为Z=FK。如果 ,则称函数列{愩n}在Z中收敛于愩,记为
,则称函数列{愩n}在Z中收敛于愩,记为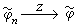 。Z空间上的连续线性泛函,称为Z空间上的广义函数,其全体记为Z′。又记J∶φ(x)
。Z空间上的连续线性泛函,称为Z空间上的广义函数,其全体记为Z′。又记J∶φ(x)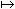 φ(-x)。
φ(-x)。
设ƒ∈K′,作Z上连续线性泛函F(ƒ)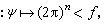 JF_1
JF_1 ∈Z,称F(ƒ)为广义函数ƒ的傅里叶变换,通常也记为愝(或形式地写成愝(σ))。傅里叶变换把K上的广义函数映为Z上的广义函数。它的逆映射称为傅里叶逆变换。广义函数的傅里叶变换理论比经典傅里叶分析提供了更为灵活和适应范围更为广阔的有力工具。
∈Z,称F(ƒ)为广义函数ƒ的傅里叶变换,通常也记为愝(或形式地写成愝(σ))。傅里叶变换把K上的广义函数映为Z上的广义函数。它的逆映射称为傅里叶逆变换。广义函数的傅里叶变换理论比经典傅里叶分析提供了更为灵活和适应范围更为广阔的有力工具。
对一元广义函数,常用的傅里叶变换列表如下:

基本空间S和S上的广义函数空间S┡
设φ(x)是Rn上的无限次可微函数,如果对于任一自然数r和 …,Pn),满足关系式
…,Pn),满足关系式 ,则称φ(x)在无穷远处是急速下降的,其全体组成的复线性空间记为S(Rn)。S中的函数序列{φm(x)}收敛于0是指对任意的r和p,
,则称φ(x)在无穷远处是急速下降的,其全体组成的复线性空间记为S(Rn)。S中的函数序列{φm(x)}收敛于0是指对任意的r和p, 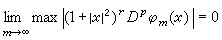 。同样称 S上的连续线性泛函 ƒ为S空间上的广义函数,也称为缓增广义函数,其全体记为S′。明显地有K嶅S,S′嶅K′。
。同样称 S上的连续线性泛函 ƒ为S空间上的广义函数,也称为缓增广义函数,其全体记为S′。明显地有K嶅S,S′嶅K′。
考虑S空间上的广义函数的好处是对于ƒ∈S′,它的傅里叶变换F(ƒ)仍是属于S′的缓增广义函数,这就给讨论带来很大方便。因此在不少应用场合多采用 S空间的广义函数。
广义函数的直积
又称张量积。设 x,y是Rn和Rm中的点,K(Rn),K(Rm)分别表示其上K 空间。ƒ∈K′(Rn),g∈K′(Rm)那么存在一个且仅有一个Rn×Rm上的广义函数,记为ƒ圱g,它由下式定义:
 式中
式中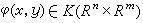 ,并且对φ(x∈K(Rn),
,并且对φ(x∈K(Rn),
 ,满足
,满足 ,称Rn×Rm上的广义函数ƒ圱g为ƒ和g的直接积。上面的定义可以看作富比尼定理的一个拓广。
,称Rn×Rm上的广义函数ƒ圱g为ƒ和g的直接积。上面的定义可以看作富比尼定理的一个拓广。
广义函数的卷积
设 ƒ,g∈K′,其中至少有一个支集有界,则可定义 K 上广义函数 
 ,称为ƒ和g的卷积(定义卷积的条件在一些情况下还可放宽一点)。对ƒ∈K′,
,称为ƒ和g的卷积(定义卷积的条件在一些情况下还可放宽一点)。对ƒ∈K′,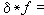
 ,
,

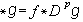 。
。
广义函数和婛∞类函数的乘积
设ƒ∈K′,α∈ (
( 是Rn上无限次可微函数),则定义广义函数αƒ:
是Rn上无限次可微函数),则定义广义函数αƒ:
<αƒ,φ>=<ƒ,αφ> (φ∈K),
称为α和ƒ的乘积,并称α为K′上乘子。当ƒ∈l*时,它和通常函数乘积相一致。
记OM(Rn)为满足下述条件的所有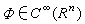 组成的线性空间:对于每个
组成的线性空间:对于每个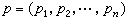 ,必存在多项式Pp(x),使
,必存在多项式Pp(x),使

称OM为在无限远点处缓增的无限次可微函数空间。OM是缓增广义函数S′的乘子空间。
如果ƒ∈S′,φ ∈OM,定义乘积φƒ为

那么φƒ仍属于S′。
但是一般地定义两个广义函数的乘积是困难的。例如两个局部可积函数的乘积就不一定是局部可积的,于是就不一定能确定为广义函数。
基本解
作为应用,广义函数论特别是它的傅里叶变换理论可有效的用来研究偏微分方程的求解问题。
设P(D)是Rn上常系数线性偏微分算子,如果能找到一个广义函数ƒ,使得P(D)ƒ=δ,那么称ƒ为P(D)的基本解或方程P(D)ƒ=0的基本解。
如果ƒ是P(D)的基本解,那么对于一般的非齐次方程
P(D)u=μ,
它的解为 u=ƒ*μ,这里μ∈K′,且假定 ƒ*μ是有意义的。事实上如 ƒ*μ存在的话,则由卷积的性质知P(D)(ƒ*μ)=P(D)ƒ*μ=δ*μ=μ。这样,基本解就可以起到构造其他解的作用。也可以利用它来讨论微分方程其他解的性质。下面是基本解的存在定理:设P为一n元多项式,那么必存在常系数偏微分方程P(D)ƒ=δ的基本解ƒ∈K′,而且这时可取ƒ,使得F(ƒ)是解析泛函。
亥维赛函数θ(x)是 的基本解。
的基本解。
此外,还可以考虑柯西问题基本解的概念。例如,称适合热传导方程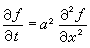 和初始条件ƒ(x,0)=δ(x)的解E(x,t)为热传导方程柯西问题的基本解。容易求得
和初始条件ƒ(x,0)=δ(x)的解E(x,t)为热传导方程柯西问题的基本解。容易求得

因此适合初始条件ƒ(x,0)=ƒ0(x)(ƒ0(x)也可以是广义函数)的热传导方程的解为
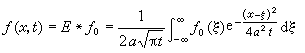 。
。
对变系数偏微分方程的研究,广义函数也同样起着很重要的作用。