常微分方程边值问题数值解法

[拼音]：changweifen fangcheng bianzhi wenti shuzhjiefa

[外文]：numerical methods for boundary value problem of ordinary differential equations

用某种离散化数值步骤求出常微分方程边值问题在离散点上的近似解的方法。各种实际问题导出不同类型的边值问题。较简单的有二阶常微分方程两点边值问题：求函数y=y(x)，x∈[α，b]，使它满足微分方程

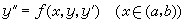
和边值条件

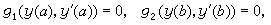
式中ƒ、g1、g2为已知函数；α与b为两个给定的端点。较一般地有一阶常微分方程组两点边值问题:求N个函数

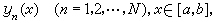
使其满足微分方程组

和边值条件

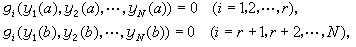
式中诸ƒn、gi是已知函数;r为给定的自然数。有些问题因求解区间是无穷区间而被称作奇异边值问题，相应的边界条件变为对解在无穷远处渐近行为的限制，例如，要求y(x)在区间[0，)上平方可积或要求当x趋于无穷时，y(x)趋于某极限值。还有些实际问题因要求解满足多个点上的条件而被称作多点边值问题。近年来，对反映边界层现象的奇异摄动边值问题提出了一些新的数值解法。此外，关于存在多个解的分歧现象数值解问题也引起人们的注意。

解常微分方程边值问题常用的数值解法有差分法和打靶法。

差分法

主要步骤是：将区间[α，b]作剖分

把微分方程差分离散化（见数值微分），加上边值条件一并构成一代数方程组，解此代数方程组即可得到边值问题的数值解。

打靶法

主要思路是:适当选择和调整初值条件，求解一系列初值问题，使之逼近给定的边界条件。如果将描述的曲线视作弹道，那么求解过程即不断调整试射条件使之达到预定的靶子，所以称作打靶法或试射法，此类方法的关键是设计选取初值的步骤。

对非线性边值问题

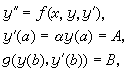
可通过下列步骤求数值解：

（1）计算初值问题

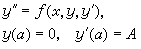
的数值解y1。若g(y1(b)，y姈(b))=B，近似地满足，则y1即为所求；否则进行②。

（2）计算初值问题

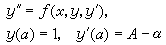
的数值解y2，若g(y2(b)，y娦(b))=B近似地满足，则y2即为所求；否则令m＝3进行③。

（3）将g(y(b)，y┡(b))视为y(α)的函数，用线性逆插值法调整初值，即计算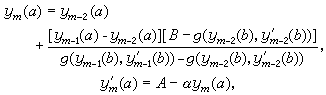然后进行④。

（4）计算初值问题

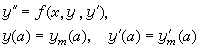
的数值解ym并进行判定：若b点边值条件近似地满足，则ym即为所求;否则令m+1崊m转向③继续计算直到满意为止。

特别地，若微分方程是线性的，则打靶法变成线性组合法，即根据常微分方程理论适当选取初值可得到一组线性独立解，利用它们的线性组合导出边值问题的解。例如线性方程边值问题

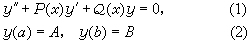
的数值解可通过两个初值问题数值解来实现。事实上，设y1(x)和y2(x)分别是方程(1)的具有初值条件和

的两个解，于是

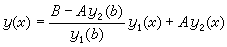
是(1)与(2)的解。

参考书目
  1. P.Henrici，Discrete variable Methods in Ordinary Differential Equations， John Wiley & Sons，New York，1962.
  2. S.M.Roberts and J.S.Shipman，Two-Point Boundary value Problems: Shooting Methods，Elsevier， New York，1972.
阅读全文