[拼音]：gangti de dingdian yundong
[外文]：motion of a rigid body about a fixed point
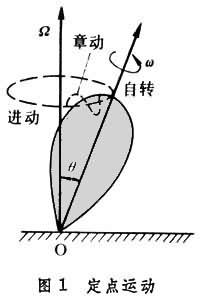
刚体上某一点始终保持不动的一种运动。如陀螺绕定点O的运动（图1）。
欧拉角
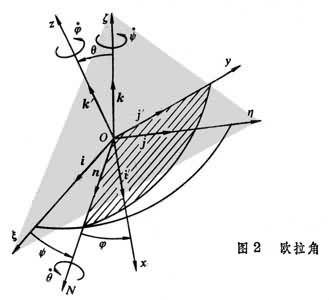
作定点运动的刚体有三个自由度。通常取如下定义的三个欧拉角作为确定刚体位置的独立参数。建立一个固结在刚体上的动坐标系Oxyz和一个以定点O为原点的定坐标系Oξηζ(图2)。定坐标系的坐标平面ξOη和动坐标系的坐标平面xOy的交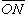线
称为节线。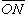和Ox轴的夹角嗞称为刚体的自转角;和Ox轴之间的夹角嗞 称为进动角;Oz轴和Oζ 轴之间的夹角θ称为刚体的章动角。嗞、嗞、θ都叫做欧拉角，因此，刚体定点运动的运动方程可用三个欧拉角的时间函数来表示：
。
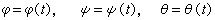刚体上点的速度和加速度设任一瞬时刚体的角速度矢量为ω，角加速度矢量为α，如取定点O为矢径原点时，则刚体上任一点P的速度矢量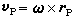
，式中rp是P点对于O的矢径。加速度矢量
。
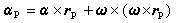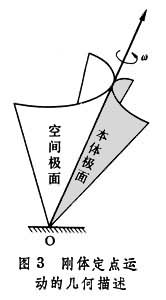
定点运动的刚体的任何有限位移可用绕过定点的某轴的一次转动而达到。因此，刚体每一瞬时运动都可看成是绕通过定点的某一瞬时转轴所作的瞬时转动，这一瞬时转轴就是该瞬时刚体角速度矢量ω的方向轴(图3)，在此瞬时转轴上的每一点的速度都是零。瞬时转轴在随刚体运动的空间中所描绘出的锥面称为本体极面。瞬时转轴在固定空间中所描绘出的锥面称为空间极面。刚体定点运动可用几何方法描述为，本体极面在空间极面上作无滑动的滚动。
欧拉运动学方程
刚体作定点运动的角速度矢量
，
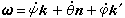式中夗、夝、夗分别为进动角嗞，章动角θ， 自转角嗞对时间t的一阶导数，它们分别称为进动角速度，章动角速度，自转角速度；k、n、k┡分别是Oζ轴，节线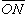
， Oz轴上的单位矢量 (图2)。把ω投影到动坐标Oxyz上得
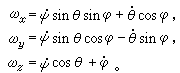
此三个方程称为欧拉运动学方程。
欧拉动力学方程如取过定点O 的刚体的三个互相垂直的惯量主轴（见惯量张量）为坐标系Oxyz的坐标轴，并设刚体对这三个坐标轴的主转动惯量分别为A、B、C。外力系对O点的主矩矢量在这三个轴上的投影分别为M x、My、Mz，则定点运动的刚体的运动微分方程为
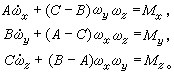
这就是L.欧拉于1758年得出的刚体定点运动的微分方程，称为欧拉动力学方程。欧拉动力学方程和欧拉运动学方程联立，在已知外力矩Mx、My、Mz和初始条件（三个欧拉角的初值和它们的初始导数值）下，可积分求得刚体定点运动的运动方程，就知道了三个欧拉角随时间变化的规律。在任意外力系的作用和任意形状刚体的情况下，这一组方程至今没有得到用求积形式表示的精确解。困难主要来自方程的非线性。但因刚体定点运动的理论分析在陀螺技术中具有重要作用，所以这个问题的解决仍然是刚体动力学的重大研究课题之一。这一组方程，目前只在下述三种特殊情况下得到了精确解：
（1）欧拉－潘索情况。作用于刚体上的外力的合力通过固定点O，则Mx、My、Mz都恒为零。此时刚体绕定点作惯性转动，欧拉动力学方程简化为
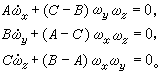
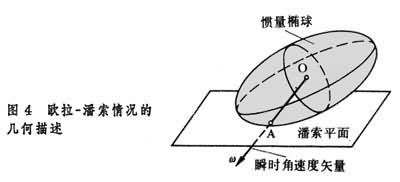
1851年L.潘索给这个情况下所得的解作了著名的几何解释:刚体运动可看成刚体关于O点的惯量椭球在一固定平面上的无滑动的滚动，此固定平面称为潘索平面（图4）。
（2）拉格朗日－泊松情况。J.L.拉格朗日于1788年给出了另一种特殊情况下的解，S.-D.泊松于1813年对此情况又作了进一步研究。他们所研究的情况是：刚体只受重力W作用，重心在Oz轴上，刚体关于O点的惯量椭球是旋转椭球，即A＝B的情况。如重心离O点的距离为d，则在此情况下欧拉动力学方程简化为
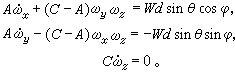
（3）柯瓦列夫斯卡娅情况。1888年俄国科学家С.Β.柯瓦列夫斯卡娅利用复变函数论的观点给出了第三种情况下的解。在此情况下:刚体只受重力W作用，重心在刚体关于O点的惯量椭球的赤道平面内，离O点的距离为d，且A＝B＝2C。此时欧拉动力学方程为
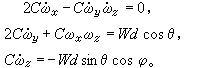
这里动坐标系的x 轴通过重心。