[拼音]:hundun
[外文]:chaos
一种貌似无规则的运动,亦作浑沌。有些非线性动力学系统具有内在随机性,它的运动对初值具有很强的敏感性,即使系统和所受外力是确定性的,即定则的(见振动),系统运动的外观却是随机的。
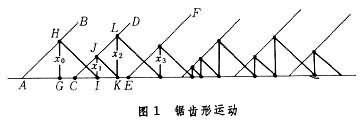
图1 是对初值有很强敏感性的一个简单数学例子。AB、CD、EF,…是一串互相平行、均匀排列的斜线段,线段与水平线的倾角均为 45°,且 AC=CE)=…=1。由AB上初始点H出发作45°斜线交水平线于I,再由I作竖直线交斜线段CD于J, 再由J作45°斜线交水平线于K,等等。令x0=GH,x1=IJ),x2=KL,…,则x1,x2,…等只决定于初值 x0。这是一个确定性动力学系统,序列(x0,x1,x2,…)代表运动,0,1,2,…,n,…是时间。系统的运动只依赖于初值,并对初值有很强的敏感性。如果初值x0=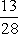 , 则这个序列是
, 则这个序列是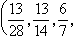
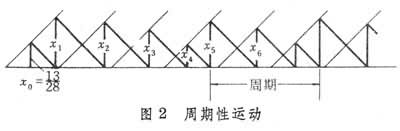
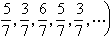 ,当n≥2时,xn+3=xn,运动是周期性的(图2)。如初值x0=
,当n≥2时,xn+3=xn,运动是周期性的(图2)。如初值x0=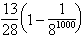 ,由于x0是有理数,且它的2
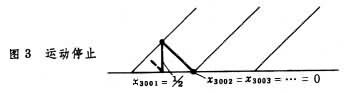
,由于x0是有理数,且它的2 倍是整数,当n≥3002时,xn=0,运动停止(图3)。如初值x0=
倍是整数,当n≥3002时,xn=0,运动停止(图3)。如初值x0=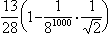 ,由于x0是无理数,运动永不停止,且是非周期的,它是同图1相仿的一个参差不齐的锯齿形波。 这三个初值的前900多位小数完全一样,但所得运动性质根本不同。由于对初值的这种极端敏感性,如果计算时没有足够的精度,在有限运算次数后运动实际上是随机的。这代表一个混沌运动。
,由于x0是无理数,运动永不停止,且是非周期的,它是同图1相仿的一个参差不齐的锯齿形波。 这三个初值的前900多位小数完全一样,但所得运动性质根本不同。由于对初值的这种极端敏感性,如果计算时没有足够的精度,在有限运算次数后运动实际上是随机的。这代表一个混沌运动。
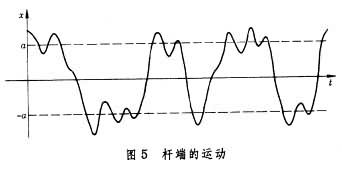
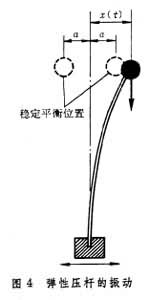
具有多个稳定平衡态的弹性系统的受迫振动中可能出现混沌响应。 设图4中的弹性压杆受到的载荷超过屈曲力,压杆的有关物理参量是确定的,且杆的基础受到确定的外来横向正弦型扰动力。理论分析和实验研究都证实,在扰动力幅度、频率取某些值时,杆端运动x(t)外观同随机运动一样 (图5)。
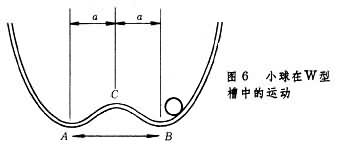
其原因可用图6 中的模型说明。弹性杆有两个稳定平衡位置,一个不稳定平衡位置,类似于图6中槽ACB中放置的小球。在受迫振动中小球什么时候跨越不稳定平衡态C,将敏感地依赖于初始条件。 其结果是出现小球在右边凹槽A处附近来因若干次后跨越C到左边凹槽B处附近,来回若干次后又跨越C,而这种来回的次数看起来是无规则的。
最早发现的混沌运动的例子是 1963年E.N.洛伦茨(1917~ )在研究天气预报中大气对流问题时提出的。他由二维的热对流运动偏微分方程出发,经过傅里叶分解、截断,并进行无量纲化,得出一个三阶的常微分方程组:
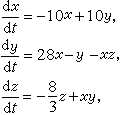
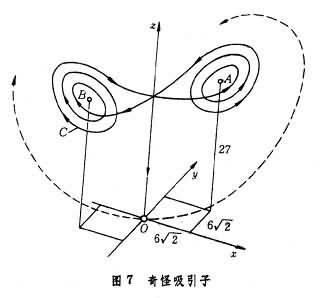
式中x,y,z都是无量纲的物理变量,x和对流速度有关,y和z则和温度分布有关;t是无量纲时间。对这组方程的数值积分表明,它的解在(x,y,z)空间中无限趋近于图7中的一个“奇怪吸引子”C,它在A、B两点周围来回盘旋,盘旋的圈数貌似无规则,因而无论x(t)、y(t)或是z(t),都是只具有统计规律性的随机过程。
在洛伦茨例子发表的同一时期,分析力学中建立了卡姆(KAM)定理,它说明接近可积哈密顿系统的运动所具有的性质。由此开始的对哈密顿系统的研究发现,当卡姆定理不适用时,系统中也出现混沌运动。在70年代,动力学系统的内在随机性理论或混沌理论以及与之相关的奇怪吸引子的数学理论都迅速发展起来。有人认为,这种理论可能是最终阐明流体力学中湍流机理的一种途径,但也有人认为目前混沌理论处理的是较简单的数学模型,对于象纳维-斯托克斯方程那样的偏微分方程还无能为力,因此,对于解决湍流机理为时尚早。在物理学和其他科学领域中,也有混沌运动的各种例子。混沌现象的发现使人们对于经典力学和统计力学之间、确定论和随机论之间的沟通,在思想上是有启发的。
- 参考书目
- 朱照宣:非线性动力学中的混沌,《力学进展》,第14卷,第2期,第129~146页,5月,1984。