[拼音]：gulizi
[外文]：soliton
又称孤立子波，是非线性波动方程的一类脉冲状的行波解。它们的波形和速度在相互碰撞后仍能保持不变或者只有微弱的变化。一个著名的例子是KdV(Korteweg-de Vries) 方程
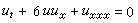的解 
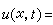
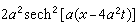。方程解的图形（见图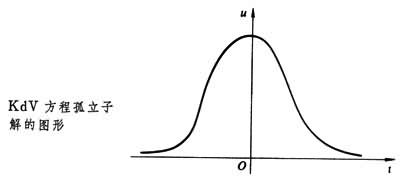
）像一个孤立的脉冲，波峰高2α2，速度为4α2。当两个这样的脉冲波沿同一方向运动时，峰高的波速度快会赶上前面峰低的波而发生碰撞。1965年M.D.克鲁斯卡尔和N.J.扎布斯基在电子计算机上作数值试验后，意外地发现两个这样的波在碰撞后，居然都能保持各自的波形和速度不变。这一性质使人联想起粒子，因之将这样的波称为孤立子(波)。早在1934年，J.S.罗素已在河流中观察到这种非线性波。现在人们已经发现很多在应用中十分重要的非线性波方程， 如正弦-戈登方程(SG方程)uxt=sinu，非线性薛定谔方程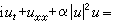
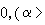
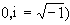等等都具有这种孤立子解。近年来，发现在等离子体光纤通信中都有孤立子现象，科学家们还认为神经细胞轴突(axon)上传导的冲动、木星上的红斑等都可以看作是孤立子。孤立子反映了自然界中一类相当普遍的非线性现象。由于孤立子同时具有波和粒子两重性质，引起了理论物理学家的极大关注，他们尝试用它来描写基本粒子。但在应用中，上述的孤立子的定义，在各种不同意义上有所放宽。
为了求解这些具有孤立子解的特殊非线性方程，自1967年起发展了一种散射反演方法。该方法的特色是将这类非线性问题的解转化为线性问题来求解，最初是C.S.伽德纳等人于1967年首先对KdV方程提出的。他们发现KdV方程和常微分算子的特征值问题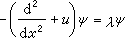 
有密切的关系。特别，若微分算子
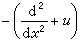中所含u（称为位势）取为KdV方程的解时，算子的特征值λ与时间t无关。于是，求解KdV方程的初值问题可以转化为求解上述特征值问题的正问题和反问题。其正问题是指已知初值u(x，0)=ƒ(x)求出与算子
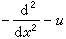的特征值等相关的一组量。这一组量称为散射量。其反问题是指已知t时刻的散射量来复原位势u(x，t)。散射量本身随时间t的演化规律十分简单，关键的步骤是求解反问题，而这一步归结为求解一个线性积分方程。伽德纳等人用这种方法成功地求出了KdV方程的单个孤立子解以及由N个孤立子叠加起来的N重孤立子解。1968年P.D.拉克斯对伽德纳等人的思想从泛函分析的角度作了十分清楚的表述，指出KdV方程可以写成lt=[A，l]形式，其中[A，l]=Al-lA，l和 A为与u有关的线性常微分算子。由于它在孤立子理论中的重要作用，后人便将它称作拉克斯方程，并将其l和A称为拉克斯对。此后又有许多人考察了一类二阶矩阵常微分算子的特征值问题，导出了与之相连的一族广泛的非线性演化方程，并建立了与该特征值问题的反问题相关连的线性积分方程。自此以后，散射反演方法逐渐发展成一种求解非线性方程初值问题的系统方法，引起了数学界的广泛重视。
除散射反演方法外，还有一种方法是利用贝克隆变换，这是一种将方程的一个解变至另一个解的变换。利用它常可从方程的平凡解(如u=0)出发，经简单积分或代数运算导出方程的一系列特解。一个经典例子是Bα：u0→u1，这里u1是由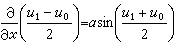
，
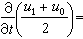
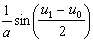确定的。只要u0是SG方程的解，则由上式可解出u1，它也是SG方程的解。式中α为自由参数。特别，取平凡解u0=0，可解得
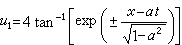，这是SG方程的一种孤立子解，称之为扭，解中的正负号分别代表两种相反的旋转方向(正扭与反扭)。贝克隆变换的一个重要性质是它的可交换性
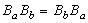，其中Bα表示参数为α的贝克隆变换。由此性质可以导出解的非线性叠加公式:
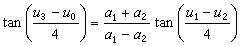，其中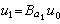
，
，
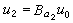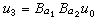。取u0=0时的u1，u2即为上述的“扭”孤立子解，代入上面的叠加公式就得SG方程的两重孤立子解
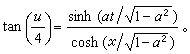
令α=ib，得
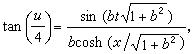
图像为正扭与反扭周期地接近又离开，如一个鼻孔呼吸，故又称“呼吸子”。应用贝克隆变换可有效地求出一些非线性方程的特解，其中有些用散射反演法难以得到;这使数学家们对寻求非线性方程的贝克隆变换产生了很大兴趣，自70年代以来已发展了好几种新的方法。
散射反演方法之所以获得成功，是因为它所处理的这类方程都可以写成一对线性方程 ψx=Uψ与ψt=Vψ的可积条件ψxt=ψtx，亦即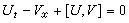
，这里U、V是某些方阵。凡是可以作为这样的关于ψ的线性方程组的可积条件的非线性方程，称为可积型的。
物理量u(x，t)的非线性演化方程的守恒律可用散度形式的微分方程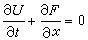
来描述，其中守恒密度U与对应流量F都是依赖于未知函数 u(x，t)的。从物理学上说，积分
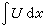就是一个不因时间而变化的物理量。无穷多个守恒律与孤立子解的存在是紧密相关的。很多具有孤立子解的非线性演化方程有无穷多个守恒律，因而也有无穷个守恒的物理量。
孤立子理论的发展，对数学和物理学都具有重要意义。物理学中的一些基本方程如规范场论中的自对偶杨－米尔斯方程、引力场理论中的轴对称稳态爱因斯坦方程，以及一系列在流体力学、非线性光学、等离子物理中有重要应用的方程，都已应用孤立子理论中的方法找到了许多有兴趣的精确解。在数学中，可积性方程的判定，及其代数性质、几何性质的研究，不仅将大大丰富偏微分方程理论本身，而且将促进一系列与之相关的分支诸如李群、辛流形、代数几何、函数论等的发展。