[拼音]:youxian danqun
[外文]:finite simple graup
除了单位元群和它本身以外没有其他正规子群的有限群。有限单群可比喻为搭成有限群的”积木块“,是有限群结构的基石。它长期是群论研究的中心问题。
有限单群分为四大类:
(1)素数p 阶循环群Zp,它包括了所有的交换单群。
(2)n个文字的所有偶置换构成的交错群An,当n≥5时是非交换单群。
(3)李型单群和李型群 李型群是复数域上单李群在有限域上的相似物,不全是单群。它包括有限域上某些典型群、例外群和扭群。前两者也称为谢瓦莱群,共有9个族,它们的记号是A(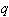 ),n≥1;B(
),n≥1;B(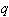 ),n>1;Cn(
),n>1;Cn(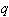 ),n>2;Dn(
),n>2;Dn(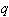 ),n>3;G2(
),n>3;G2(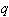 );F4(
);F4(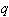 );E6(
);E6(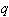 );E7(q);E8(
);E7(q);E8(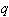 )。这里
)。这里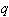 =pm,p是素数。以下的q也有此意义。
=pm,p是素数。以下的q也有此意义。
除了A1(2)、A1(3)、B2(2)、G2(2)外,这些群对其中心的商群都是有限单群。这些群中的大部分,E.伽罗瓦、C.若尔当、L.E.迪克森等已早有研究。直到1955年,C.谢瓦莱对任意有限域 GF(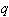 )构造出复数域上单李群的相似物,用统一的方法证明了这些群的存在性、单纯性和其他性质。
)构造出复数域上单李群的相似物,用统一的方法证明了这些群的存在性、单纯性和其他性质。
扭群共七族,它们是2An(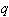 ),n>1;2B2(
),n>1;2B2(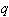 ),
),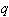 =2
=2 ;2Dn(
;2Dn( ),n>3;3D4(q);2G2(
),n>3;3D4(q);2G2( ),
), =3
=3 ;2F4(
;2F4( ),
), =2
=2 ;2E6(
;2E6( )。除了2A2(2)、2B2(2)、2G2(3)、2F4(2)外,它们都是单群。而2F4(2)的换位子群(2F4(2))┡还是不在以上几族中的一个特殊单群。
)。除了2A2(2)、2B2(2)、2G2(3)、2F4(2)外,它们都是单群。而2F4(2)的换位子群(2F4(2))┡还是不在以上几族中的一个特殊单群。
利用谢瓦莱群的图自同构和域自同构可以统一地得到所有扭群,如R.施坦伯格、铃木通夫、R.雷和J.蒂茨等人的工作。
在以上群中An( )、Bn(
)、Bn( )、Cn(
)、Cn( )、2An(
)、2An( )分别同构于GF(
)分别同构于GF( )上的典型群PSLn+1(
)上的典型群PSLn+1( )、PΩ2n+1(
)、PΩ2n+1( )、PSP2n(
)、PSP2n( )和PSUn(
)和PSUn( )。而Dn(
)。而Dn( )和2Dn(
)和2Dn( )分别同构于
)分别同构于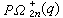 和
和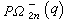 (对每个
(对每个  有两族2n维的正交群,以“+”和“-”两个符号来区别)。谢瓦莱群中的G2(
有两族2n维的正交群,以“+”和“-”两个符号来区别)。谢瓦莱群中的G2( )、F(
)、F( )、E6(
)、E6( )、E7(
)、E7( )、E8(
)、E8( )则是例外群。
)则是例外群。
(4)零散单群 凡不属于以上三类的有限单群, 称为零散单群,共有26个。É.L.马蒂厄于1860年和1873年先后得到5个多重传递置换群M11(4重)、M12(5重)、M22(3重)、M23(4重)和M24(5重),它们都是零散单群。一百年之后,Z.简科于1965年才发现了另一个新的零散单群,记为J1。尔后陆续地发现了所有的零散单群,仿照前者,一般以重要发现者的姓的前面字母来记各零散单群,若同一人发现多于一个这样的群时则加上数字的下标,它们是

最大的零散单群为F1,名为怪物群或魔群,它的阶为 246·320·59·76·112·133·17·19·23·29·31·41·47·59·71,约为1054。G.格里斯用手算,从47·59·71=196883维的线性表示而得到F1。它有着良好的内在的几何结构,并且有20个左右的零散单群作为它的子群,所以并不是什么怪物,G.格里斯改称它为“友好巨人”。
研究有限单群的一般方法,可非常概括地归结为以下几种:
(1)模特征标论和特殊特征标论方法,前者为R.(D.)布饶尔所创,后者为布饶尔和铃木通夫所创。
(2)p局部子群分析法。它是由J.G.汤普森等人建立和发展起来的研究非单位 p子群的正规化子的方法。
(3)几何分析法及其发展。此法是由B.费希尔和M.阿施布歇尔等所创。
有限单群的完全分类,即找出有限单群所有的同构类,经全世界上百名的数学家约40年的共同努力,终于在1981年得到解决,这是数学史上的又一个非凡成就。有限单群分类的整个论证用了5000页以上的篇幅,散布在超过300篇文章之中,引用了很多新的群论概念和证明了大量的定理。历史上的一些重要进展,可以概述如下:
20世纪初,W.伯恩赛德关于pαqъ阶群(p、 是素数)必是可解群的定理,是有限单群分类问题早期最重要的工作。它说明非交换有限单群的阶至少有三个不同的素数。三四十年代之交,布饶尔开始利用他所创造的模特征标理论来研究有限单群问题,在这期间,段学复随布饶尔研究了阶含素数p仅为一次的群及其模特征标,1942年,他们一起完成了10000阶以下的单群分类。1945年合写了“论有限单群”的论文。他们的一些结果至今还被人引用,有的得到推广。1954年布饶尔关于对合的中心化子的定理,即设τ是偶阶单群G的一个对合即二阶元素,CG(τ)是其中心化子,则
是素数)必是可解群的定理,是有限单群分类问题早期最重要的工作。它说明非交换有限单群的阶至少有三个不同的素数。三四十年代之交,布饶尔开始利用他所创造的模特征标理论来研究有限单群问题,在这期间,段学复随布饶尔研究了阶含素数p仅为一次的群及其模特征标,1942年,他们一起完成了10000阶以下的单群分类。1945年合写了“论有限单群”的论文。他们的一些结果至今还被人引用,有的得到推广。1954年布饶尔关于对合的中心化子的定理,即设τ是偶阶单群G的一个对合即二阶元素,CG(τ)是其中心化子,则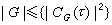 。于是,从已知偶阶单群的对合的中心化子出发,最多构造出有限多个单群。可用这结果去发现和构造一些新单群,许多零散单群就是这样发现的;更重要的是可以用中心化子来刻划群的构造,用于单群分类。这一定理标志了单群分类的新起点,而被称之为布饶尔纲领。布饶尔是近代有限单群分类工作的先驱。
。于是,从已知偶阶单群的对合的中心化子出发,最多构造出有限多个单群。可用这结果去发现和构造一些新单群,许多零散单群就是这样发现的;更重要的是可以用中心化子来刻划群的构造,用于单群分类。这一定理标志了单群分类的新起点,而被称之为布饶尔纲领。布饶尔是近代有限单群分类工作的先驱。
1962年,W.费特和汤普森关于奇阶群必为可解群的定理是单群分类中最重要的一个定理,它标志着有限单群分类的重大突破,也是第一篇长文章(225页之多)。汤普森在文中初步建立并运用了p局部子群分析法,其后于1968~1974年间,他在关于极小单群(即所有真子群皆为可解群)及更一般的单N群(即所有p局部子群皆为可解群)的分类定理的证明中,完善了 p局部子群分析法。
1972年,D.戈朗斯坦提出的有限单群分类方案或计划,指出了如何才能实现有限单群的完全分类。虽然这个计划在后来作了某些修改,但是此后美、英、德、日等国的群论学家自发地组织起来按计划去攻克这个大问题,终于以10年左右的时间取得了数学史上的这项重大的成果。
有限单群分类问题的解决对有关问题的影响非常深远,有些长期存在的群论问题已经由于它的解决而解决或可以解决。例如,①O.施赖埃尔猜想有限单群的外自同构群是可解的。
(2)有限单群皆可由两个元素生成;有限非交换单群的元素皆为换位子。
(3)除Sn和An外,不存在k≥6重传递置换群;所有双重传递群已被决定;所有素数p次置换群已知。
下述有限单群问题正在被研究并取得进展:
(1)整理和简化有限单群分类问题的全部论证。
(2)研究F1和模函数的关系,进而研究哪些单群能作为有理数域上的伽罗瓦群。
(3)用分类的结果去解决群论以及其他的数学问题,这种应用正迅速增加。
(4)进一步计算有限单群的常、模特征标和子群等。
- 参考书目
- D. Gorenstien,Finite Simple Groups, Plenum Press, New York, 1982.
- D.Gorenstien,Classifying the Finite SimpleGroups,Bulletin (New Series)of the American MatheMatical Society, 14, pp. 1~98, 1986.