[拼音]：liangzichanglun
[外文]：quantum field theory
根据量子力学原理建立的场的理论，是微观现象的物理学基本理论。场是物质存在的一种基本形式。这种形式的主要特征在于场是弥散于全空间的。场的物理性质可以用一些定义在全空间的量描述〔例如电磁场的性质可以用电场强度和磁场强度或用一个三维矢量势A(X，t)和一个标量势嗘(X，t)描述〕。这些场量是空间坐标和时间的函数，它们随时间的变化描述场的运动。空间不同点的场量可以看作是互相独立的动力学变量，因此场是具有连续无穷维自由度的系统。场论是关于场的性质、相互作用和运动规律的理论。量子场论则是在量子物理学基础上建立和发展的场论，即把量子力学原理应用于场，把场看作无穷维自由度的力学系统实现其量子化而建立的理论。量子场论是粒子物理学的基础理论并被广泛地应用于统计物理、核理论和凝聚态理论等近代物理学的许多分支。
量子场论的建立及基本概念在经典场论（例如J.C.麦克斯韦的电磁场论）中场量满足对空间坐标和时间的偏微分方程，因此经典场是以连续性为其特征的。按照量子物理学的原理，微观客体都具有粒子和波、离散和连续的二象性。在初等量子力学中对电子的描述是量子性的，通过引进相应于电子坐标和动量的算符和它们的对易关系实现了单个电子运动的量子化，但是它对电磁场的描述仍然是经典的。这样的理论没有反映电磁场的粒子性，不能容纳光子，更不能描述光子的产生和湮没。因此，初等量子力学虽然很好地说明了原子和分子的结构，却不能直接处理原子中光的自发辐射和吸收这类十分重要的现象。1927年P.A.M.狄喇克首先提出将电磁场作为一个具有无穷维自由度的系统进行量子化的方案。电磁场可以按本征振动模式作傅里叶分解，每种模式具有一定的波矢k，频率ωk和偏振方式s=1，2、ωk=|K|с。因此自由电磁场(不存在与其相互作用的电荷和电流)可以看作无穷多个没有相互作用的谐振子的系统，每个谐振子对应于一个本征振动模式。根据量子力学，这个系统具有离散的能级
nk，s=0，1，2，…，是非负整数。对基态，所有的 nk，s=0，激发态表现为光子，nk，s是具有波矢k极化s的光子数，啚ωk是每个光子的能量。还可以证明啚K是光子的动量，极化s对应于光子自旋的取向。按照普遍的粒子和波的二象性观点，应当可以在同样的基础上描述电子。这要求把原先用来描述单个电子的运动的波函数看作电子场并实现其量子化。与光子不同的是电子服从泡利不相容原理。1928年E.P.约旦和E.P.维格纳提出了符合于这个要求的量子化方案。对于非相对论性多电子系统，他们的方案完全等价于通常的量子力学，在量子力学文献中被称为二次量子化。但是，这个方案可以直接推广到描述相对论性电子的狄喇克场ψα，α＝1，2，3，4，量子化自由电子场的激发态相应于一些具有不同动量和自旋的电子和正电子，每个状态最多只能有一个电子和一个正电子。下一步是考虑电磁场与电子场的相互作用并把理论推广到其他的粒子，例如核子和介子。描述电子场和电磁场相互作用的量子场论称为量子电动力学，它是电磁作用的微观理论。1929年W.K.海森伯和W.泡利建立了量子场论的普遍形式。按照量子场论，相应于每种微观粒子存在着一种场。设所研究的场的系统可以用N个互相独立的场量嗘i(X，t)(i=1，2，…，N)描述，这里X是点的空间坐标，t是时间。各点的场量可以看作是力学系统的无穷多个广义坐标。在力学中可以定义与这些广义坐标对应的正则动量，记作πi(X，t)。根据量子力学原理，引入与这些量对应的算符拤i(X，t)和挸i(X，t)。对于整数自旋的粒子，可以按照量子力学写出这些算符的正则对易关系。对半整数自旋的粒子则按照约旦和维格纳的量子化方案，用场的反对易关系。在给定由拤i和挸i组成的哈密顿算符后，可以按量子力学写出场量满足的海森伯运动方程式，它们是经典场方程的量子对应。量子力学还给出计算各种物理量的期待值以及各种反应过程的几率的规则。像通常力学中的情形一样，也可以等价地选取其他的广义坐标，例如取场量嗘i(X，t) 的傅里叶分量作为广义坐标。在用到自由电磁场时，就得到前面已经叙述的结果。量子场论的这种表述形式称为正则量子化形式。量子场论还有一些基本上与正则量子化形式等价的表述形式，其中最常用的是R.P.费因曼于1948年建立并在后来得到很大发展的路径积分形式。在进行场的量子化时，必须使理论保持一定的对称性。在涉及高速现象的粒子物理学中，满足相对论不变性是对理论的一个基本要求。除此以外，还必须保证所得的结果符合量子统计的要求，即符合正确的自旋统计关系。在量子场论中这些要求都达到了。在量子场论的框架内出了自旋统计关系的一般证明。量子场论给出的物理图像是：在全空间充满着各种不同的场，它们互相渗透并且相互作用着；场的激发态表现为粒子的出现，不同激发态表现为粒子的数目和状态不同，场的相互作用可以引起场激发态的改变，表现为粒子的各种反应过程，在考虑相互作用后，各种粒子的数目一般不守恒，因此量子场论可以描述原子中光的自发辐射和吸收，以及粒子物理学中各种粒子的产生和湮没的过程，这也是量子场论区别于初等量子力学的一个重要特点。所有的场处于基态时表现为真空。从上述量子场论的物理含义可以知道真空并非没有物质。处于基态的场具有量子力学所特有的零点振动和量子涨落。在改变外界条件时，可以在实验中观察到真空的物理效应。例如在真空中放入金属板时，由于真空零点能的改变而引起的两个不带电的金属板的作用力（卡西米尔效应）以及由于在外电场作用下真空中正负电子分布的改变导致的真空极化现象。量子场论本质上是无穷维自由度系统的量子力学。在量子统计物理和凝聚态物理等物理学分支中，研究的对象是无穷维自由度的系统。在这些分支中，人们感兴趣的自由度往往不是对应于基本粒子的运动而是系统中的集体运动，例如晶体或量子液体中的波动。这种波动可以看作波场，而且它们也服从量子力学的规律，因此量子场论同样可以应用于这些问题。
在考虑相互作用后，目前一般还不能求得量子场论方程的精确解，必须采用近似计算方法。较早发展起来的量子场论的计算方法是在量子电动力学中首先采用的微扰的方法。在量子电动力学中，考虑到电子场和电磁场相互作用的耦合常数(即电子的电荷) e是一个小量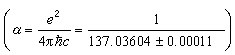
，把哈密顿量中代表相互作用的项作为对自由场哈密顿量的微扰来处理。这样各种反应过程的振幅可表成耦合常数 e的幂级数，微扰论方法是逐阶计算幂级数的系数。考虑到耦合常数很小，只要计算幂级数的前面几个低次项，就可以得到足够精确的近似结果。在一般的量子场论问题中，如果耦合常数足够小，也可以类似地用微扰论的方法处理。1946～1949年朝永振一郎、J.S.施温格和费因曼等人发展一套新的微扰论计算方法，这种微扰论方法具有形式简单、便于计算并且明显保持相对论协变性的优点。特别是，费因曼引入了图形表示法和相应的物理图像，提供了写出微扰论任意阶项的系统的方法──而且这种方法有很强的直观性。
在用量子电动力学计算任何物理过程时，尽管用微扰论最低级近似计算的结果和实验是近似符合的，但进一步计算高次修正时却都得到无穷大的结果。同样的问题也存在于其他的相对论性量子场论中，这就是量子场论中著名的发散困难。它的根源在于：在现在的相对论性量子场论中，微观粒子实际上被看作一个点。即使在经典场论中，如果把电子看作一个点，由电子产生的电磁场对本身的作用而引起的电磁质量也是无穷大的。在量子场论中发散有更多的形式，它们都起源于粒子产生的场对本身的自作用。发散困难的存在表示现在的量子场论不能应用到很小的距离。曾经有不少修改量子场论基本假设的尝试，但都不成功。除这种尝试外，还应当注意到微观粒子可能并不真正是基本的，它们如果具有占有一定体积的内部结构，也必须会改变点粒子场论在小距离处的结果。在现有量子场论的框架内，发散困难用重正化的方法得到部分的解决。现有的量子场论可以分为两类。在第一类场论中所有的发散因子都可以归结为少数几个物理参量的发散。如果重新调整这几个参量，使它们取实验要求的数值，对其他的物理量仍可用现有的理论计算，如果按重正化的耦合常数作微扰展开就可以得到有限的结果。这类理论称为可重正化的。量子电动力学属于这一类。在量子电动力学中，只有电子的质量和电荷需要重正化。重正化计算的合理性在于：如果理论需要作的修改只限于充分小的距离范围之内，这些不发散的物理量受到的影响是很小的。另一类理论中有无穷多个物理参量发散，这类理论称为不可重正化的。至少现在还没有办法用不可重正化的理论作包括粒子自作用的计算。1949年左右，施温格和费因曼等人首先用新式的微扰论作量子电动力学中的重正化计算。重正化的普遍理论及其严格证明经过H.H.博戈留博夫、O.C.帕拉修克、K.赫普和W.齐默尔曼等人的研究在60年代中才完成。量子电动力学的重正化微扰论计算在很高的精度上与电子和μ子的反常磁矩（见μ子和电子回磁比）及原子能级的兰姆移位的实验符合，迄今量子电动力学通过了所有实验的考验，这些实验表明量子电动力学在大于10-16cm处是正确的。量子电动力学的成功是重正化量子场论的实验证实。
非微扰方法处理量子场论问题的微扰论方法有它的局限性，它要求耦合常数很小，即属于弱耦合的情况。耦合强到一定程度后微扰论展开式的头几项就不再是好的近似。因此在量子场论发展过程中已经针对不同问题的需要发展了许多种非微扰方法，如色散关系理论、公理化场论、流代数理论、半经典近似方法、重正化群方法、格点规范理论等。这些方法的出发点各不相同，基本上可以归为两类。一类是直接根据场论的基本原理和普遍的对称性要求，给出一般的限制和预言。这类理论的典型例子是色散关系理论和公理化场论。这种做法虽然比较严格，但正因为是普遍的讨论，就不可能对许多具体问题作出细致的回答，所得的结果有很大的局限性。另一类是找寻另一种近似方案，用另一个小参量代替耦合常数来作某种近似处理。因为作近似时不再以耦合常数的幂次为依据，所以有时对强耦合也能应用。例如，格点规范理论的强耦合展开式就带有这样的特点。这样的理论虽然可以解除微扰论所受的限制，但却受这种理论本身所取近似条件的限制。现在还没有非常有力的非微扰方法。近年来在格点规范理论的研究中发展了用有限的点阵上的量代替无限的连续的时空中的场，利用电子计算机作蒙特—卡罗模拟的方法。虽然这不再是无穷维自由度的系统，如果所取点阵的尺度与所研究的现象有关的主要过程作用的范围相当，它不失为一种量子场论的近似方法。
量子场论的发展及其在物理学各分支中的应用量子场论作为微观现象的物理学基本理论广泛应用于近代物理学各个分支。粒子物理学的发展不断提出场论研究的新课题，并取得了进展，它包括复合粒子场论、对称性自发破缺的场论、非阿贝耳规范场论和真空理论的新发展等几个互相联系着的方面。在研究这些问题时广泛应用了量子场论的路径积分和泛函的表达形式。自60年代后期以来规范场的研究成为场论研究的一个中心，已经解决了这类理论所特有的量子化和重正化方面的问题，阐明了规范场的一些特殊性质。1961年至1968年S.L.格拉肖、S.温伯格和A.萨拉姆建立的描述统一的弱作用和电磁作用的自发破缺规范理论，在1978年至1983年已经基本上得到实验的证实。量子色动力学作为描述强作用的规范理论也取得了一定的成就，被认为是有希望的强作用基本理论。在量子电动力学取得成功以后，量子场论在粒子物理学中取得的这些新成就使人们相信；虽然存在着发散困难这样的基本问题和在强耦合下缺少有效的近似方法的困难，量子场论仍然是解决粒子物理学问题的理论基础和有力工具。现在除规范场论中的一些问题例如所谓囚禁问题仍然是人们注意的中心外，一些新的课题如引力场量子化、超对称性量子场论等正吸引着人们去进行研究。在统计物理、凝聚态理论和核理论中广泛地采用量子场论的格林函数和费因曼微扰论方法，它们已经成为这些物理学分支的基本理论工具。费因曼微扰论方法使得人们可以在微扰论展开式中分出一部分对所研究的现象起主要作用的项来作部分求和，大大提高了人们解决各种问题的能力。量子场论方法对温度不为零的统计物理学以及超导和量子液体等现象的理论发展起了非常重要的推动作用。统计物理学中有些现象本质上不一定是量子效应，但由于是无穷维自由度的问题，它们与量子场论问题在数学形式和物理内容上都有十分相似之处。量子场论方法对这些问题也有重要的应用。例如，重正化群方法的思想和工具对解决统计物理学中长久未能解决的临界现象问题起了关键性的作用。正因为量子场论已成为近代物理学各分支的共同基础理论，量子场论的任何一个重要进展都会对不只是一个分支的发展有重要的推动作用。