代数稳定判据

[拼音]：daishu wending panju

[外文]：algebraic stability criterion

根据系统特征多项式的系数直接判断系统稳定性的判据。系统的特征多项式就是系统传递函数的分母多项式，它是复变数s的一个代数多项式,使这一多项式为零而求得的s值称为特征多项式的根。代数稳定判据只适用于线性定常系统（见线性系统、定常系统）且其特征多项式能给出的情况。线性定常系统稳定的充分必要条件，是其特征多项式的根均具有负实部，亦即均位于不包含虚轴的左半s复数平面内。代数稳定判据的优点是可以避免求根的复杂过程，直接根据多项式的系数的一些代数运算，来判定系统是否满足上述稳定条件。

必要条件

若系统的特征多项式为

其中a₀，a₁，…，a_n均为实数,则系统为稳定的必要条件是系数a₀，a₁，…，a_n均为正数。

劳思判据

1875年英国数学家E.J.劳思所建立，根据D(s)的系数组成如下的劳思表。

系统为稳定的充分必要条件是劳思表的第一列元素C₁₁、C₁₂、C_1n、C_1n+1均为正数。

胡尔维茨判据

1895年德国数学家A.胡尔维茨所建立。根据D(s)的系数组成如下的n×n胡尔维茨矩阵：

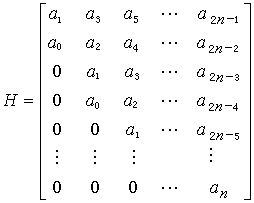
其中下标指数大于 n的元均用零代替。系统为稳定的充分必要条件是矩阵H的一切顺序主子式和a₀均为正数，即△₀=a₀>0,△₁=a₁>0,△₂=a₁a₂-a₀a₃>0,…,△_n=|H|>0。其中│H│表示矩阵H的行列式。理论研究表明，胡尔维茨判据实质上与劳思判据是完全等价的。

代数稳定判据的其他应用

除了判断系统的稳定性，代数稳定判据尚可用于：

（1）确定不稳定系统特征多项式的正实部根的数目：它等于劳思表中第一列的各系数符号的改变次数。

（2）判断系统是否具有所期望的衰减度:设期望衰减度为e^-αt(α >0)；则取s=λ-α 并代入D(s),可得出以λ为待定量的新多项式β(λ)。对β(λ)运用代数稳定判据，如果稳定就意味着系统具有期望的衰减度，否则就不具有期望衰减度。

（3）建立参数稳定域：对D(s)中包含的一个或几个可变动系数，通过应用代数稳定判据可确定出系统为稳定时的系数范围，由此可构成参数稳定域。