点涡

[拼音]：dianwo

[外文]：point vortex

无限长直线涡管元（见涡旋）在与其垂直的平面中表现为一个点涡。考虑孤立点涡对周围无界的无粘性不可压缩流体所诱导的速度场。在流动平面上取极坐标(r，嗞)，原点放置在点涡处。点涡的强度为г。根据对称性可知点涡所诱导的速度只有嗞方向的分量v_嗞，且v_嗞=v_嗞 (r)。对以 O为心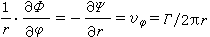，为半径的圆，用联系速度环量和涡通量的斯托克斯公式得v_嗞=г／2πr。由此可见，速度与半径成反比， 在点涡处趋于无限大， 所以点涡本身是一个奇点。由于点涡外的流动处处无旋且流动为轴对称，因此存在着速度势 ф和流函数 Ψ，它们和速度之间存在关系，积分后得到：

。

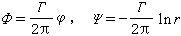与之对应的复变解析函数的表达式为：

，

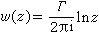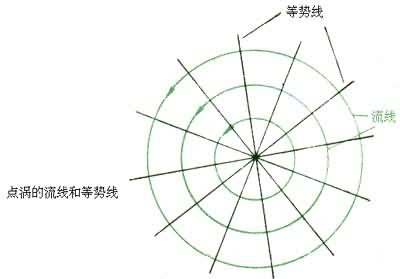
式中z为复变量；ω(z)称为复位势。根据ф和Ψ的表达式易见流线是以点涡为心的同心圆族，等势线是发自原点的射线族（见图）。 г>0对应于逆时针方向旋转的点涡;г<0对应于顺时针方向旋转的点涡。

龙卷风是点涡的一个例子。在龙卷风的中心附近，流动速度很高，压力很低。

在平面无旋流动中，点涡是一个重要的基本流子，它和均匀流、源流、偶极子流等基本流子联合使用常能得到很多有实际背景的流动。又如，将轴线某线段上的点涡连续分布、点源连续分布和均匀流叠加可得薄翼绕流问题的解。一般说来，对于运动物体所受举力的问题，在使用奇点分布法求绕流问题的解时，常需采用点涡这种形式的基本流子，因为举力同速度环量有着密切的关系。

在粘性不可压缩流体中有一类特殊流动，其速度分布同点涡所诱导的速度分布完全相同。 一半径为 r₀的直圆柱体在粘性不可压缩流体中绕轴旋转，圆周上的切向速度为 v₀，令 г=2πr₀v₀。由于粘性的作用，圆柱的旋转将带动不同半径上的流体绕轴旋转，其速度分布为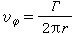，即速度值随半径r的增加成反比地减小。令圆柱半径趋于零，同时要求г保持一常数值，结果得到一根半径无限小的刚性柱体在粘性流体中的运动，它所产生的流场和点涡所诱导的完全等同。