[拼音]：feibiaozhun fenxi
[外文]：non-standard analysis
美国数学家、逻辑学家A.鲁宾孙于1960年所开创的一门新兴的数学学科。鲁宾孙利用现代数理逻辑的概念和方法证明了实数结构 R可以扩张为包含无穷小与无穷大数的结构*R，在一定意义下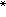
R与R具有相同的性质。更确切地说，他用模型论的方法给出了包括经典数学分析（又称分析学，也称标准分析）在内的R的完全理论的非标准模型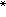R。它使G.W.莱布尼茨的无穷小问题得到圆满的解决。狭义地说，利用R和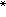R的互相转换来研究数学分析的方法叫做非标准分析。一般地，凡是对某类数学对象用类似于上述的扩张来进行的研究都称为非标准分析。现在这种方法（称为非标准方法）已成功地应用于数学的各个分支。
称
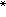R中的元素为超实数，除包含普通实数外，还包含无穷小（绝对值小于任何正实数的数）、无穷大（绝对值大于任何正实数的数）和有限超实数（绝对值小于某一正实数的数）。对超实数和对实数一样，可以施行加、减、乘、除等运算，而且适合实数的各种运算法则（如加法和乘法的结合律与交换律等）；还可以按大小顺序排列在一条几何直线上。形象地加以描述，可如图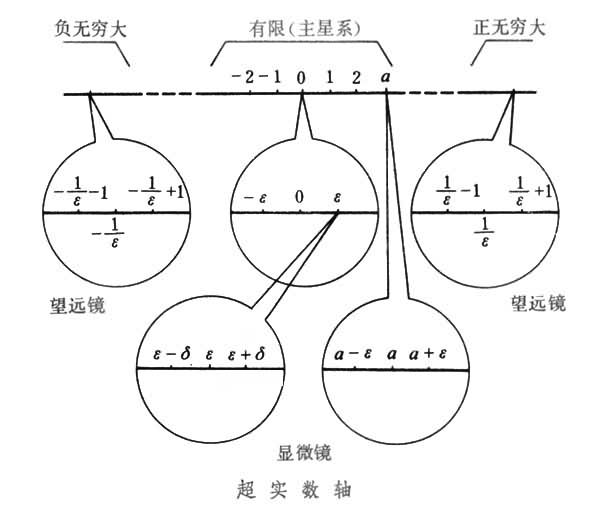
所示。
把表示超实数系的直线称为超实数轴。超实数轴上，表示有限超实数的范围称为主星系。此外还有无限多个星系，它们中的每个点都对应一个无穷大数，而且每个星系中的任何两个数都相差一个有限数。普通实数轴上的每个点，对应超实数轴上主星系上的一个单子。每个单子内的任何两个超实数之差是一个无穷小，而且这些无穷小具有无限多个不同的阶(层次)。就有限数范围而言，每个单子内恰包含一个普通实数，称为标准数。不是普通实数的超实数称为非标准数。如果两个超实数α与β相差是一个无穷小，就称α无限接近于β，记为α埍β。显然，这是一个等价关系。因此，每个有限超实数α无限接近于一个标准数α（即α埍α）。也就是说α＝α+ε，其中ε为一无穷小。α称为 α的标准部分，记为0α或stα。只有0既是标准数，又是无穷小。显然，任何有限个无穷小之和总是小于 1，就是说超实数域不满足阿基米德性质(即对于任意的正数α与b，总存在着一个自然数n，使得nα≥b)。
非标准分析在严格的数学基础上恢复了莱布尼茨的作为“更合于发明家的艺术”的无穷小方法。这个方法无论在刻画概念、证明定理、思考问题等方面都显示出优越性。下面的举例中用到的函数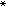
ƒ(x)是 R中的函数ƒ(x)在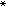R中的自然扩张， 区间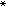[α，b]是R中的区间[α，b]在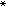R中的自然扩张。
连续:函数ƒ(x)在标准点x0上连续，当且仅当x埍x0时，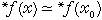
。
一致连续:函数ƒ(x)在〈α，b〉(各种区间)上一致连续，当且仅当，若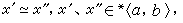
有
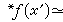
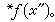
导数：设函数ƒ(x)在标准点x0附近有定义，而且如果对于x0的单子内的所有x≠x0，超实数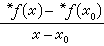
有相同的标准部分
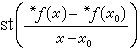，就称ƒ(x)在x0处是可导的，而称标准实数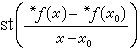为ƒ(x)在点x0处的导数，记为
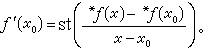
积分:设函数ƒ(x)在区间[α，b]上是连续的，它在[α，b]上的定积分是
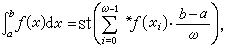
式中 ω是一任意无穷大自然数，分点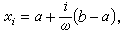
0≤i<ω。
可以证明，以上这些概念的非标准定义与相应的标准定义是完全等价的。下面用无穷小方法论证一个熟悉的定理：在有限区间[α，b]上的连续函数ƒ(x)是一致连续的。设x┡与x″是 [α，b]上任意的两个超实数，且x┡埍x″。由于
[α，b]是有限闭区间，所以必存在一个标准点x0∈[α，b]使得x┡埍x0，又因为埍是一等价关系，因此，x″埍x┡埍x0。由ƒ(x)的连续性知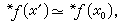
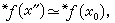所以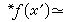
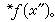
由此可以看出，用无穷小方法，可使许多概念的刻画显得直观、简明，可使定理的论证缩短。
在非标准分析中有重要的转换原理:每一个关于R可形式化的命题对R成立者，经适当解释对
R也成立，反之亦然。这里，“适当解释”是指在命题中出现的对象(如集合、关系、函数等)在R中都被解释为相应的内对象。有了这条转换原理，就可以借助于标准分析以了解非标准结构并运用非标准分析来解决标准分析的问题。除了转换原理外，在非标准分析中还有两条重要的原理，即理想化原理和标准化原理。
在17世纪微积分学的初创时期，人们就注意到这门学科的基础问题。I.牛顿和莱布尼茨都曾使用过无穷小，尤其是莱布尼茨及其跟随者，在一阶和高阶无穷小的基础上，发展了微积分理论；他们完全允许引进无穷小和无穷大，而且把它们看做是类似于虚数的理想元素，这些理想元素服从于普通实数的定律。他们所用的记号，在欧洲大陆上被广泛采用。这些记号的优越性，促进了当时微积分理论在欧洲大陆上迅速发展。因此，鲁宾孙把莱布尼茨视为非标准分析的真正先驱者。但是这个理论却存在着显著的内在矛盾──有时把无穷小看作非零而作除数，有时又把它看作是零而舍去。局限于当时的条件，这个矛盾一时还不能彻底解决，难免受到非难和攻击。英国的主观唯心主义哲学家B.贝克莱(1685～1753)主教在1734年著文攻击无穷小为“消失了的量的幽灵”。直到19世纪，A.-L.柯西、B.波尔查诺和K.（T.W.）外尔斯特拉斯用极限理论为数学分析建立了逻辑上严谨的基础，从而促进了数学分析的大发展。此后，无穷小和无穷大在分析学中就再也没有地位，只剩下了诸如“某变量趋于无穷大”这一类的说法而已。极限理论虽然使得数学分析获得了逻辑的严谨性，但是却失去了无穷小方法的简明性和直观性。正因为无穷小方法便于缩短论证，“更合于发明家的艺术”，所以直到今天，许多物理学家、经济学家和工程师仍习惯于运用无穷小方法。然而，数学家们却认为在数学分析中作为数的无穷小是不存在的。直到20世纪60年代，鲁宾孙运用数理逻辑严谨地论证了无穷小的存在性，圆满地解决了莱布尼茨的“无穷小的矛盾”的问题，开创了非标准分析。接着W.卢森堡用超幂方法构造了非标准模型，以后又构造了多饱和模型。此后，非标准分析发展很快，现在已成功地应用到许多方面，如点集、拓扑学、测度论、函数空间、概率论、微分方程、代数数论、流体力学、量子力学、理论物理和数理经济等。非标准分析为具有众多的小额贸易的商业市场提供了一个很好的模型。还有，它对模拟一个在边界为无穷大的容器中的压力下进行气体的热力学过程是很有成效的。非标准分析对某些学科中出现的一些困难问题已经作出有益的贡献。例如，用非标准分析方法首先解决了几十年未解决的希尔伯特空间上的多项式紧算子的不变子空间的存在问题；又如，中国数学家用非标准分析方法给出了解决广义函数的乘法问题的一个富有成效的方法；再如，法国数学家对常微分方程的奇异摄动已做出了大量很有意义的成果。还须指出，除非标准分析外，使得无穷小与无穷大能在分析学中使用的还有种种尝试。在这方面最有成效的有D.劳格维茨的无穷小数和中国学者提出的广义数的研究。