[拼音]：duoyuan weijifenxue
[外文]：differential and integral calculus for functions of several variables
关于多元函数的微积分学，是微积分学的一个组成部分。它是体现在一元函数的微分学和积分学中的基本概念和计算方法在应用到多元函数的情形的发展。在这发展中，基本概念都被推广到多元的情形，而计算方法则被化归到一元的情形。从而计算仍旧是在实数范围内进行。这样，多元微积分学的基本任务便在于，以一元微积分学为基础，来阐述其中基本概念和计算的规律对于任意多个变量的函数仍然一致有效，同时分析由于变量个数的增多而带来的特点。
把一元函数的研究扩展到多元函数
的这两个基本任务，都在n=2的情形中便已表现出了它们的一般性；所以主要就二元函数u=ƒ(x，y)进行叙述，只是在进一步展示新的特点有需要时才考虑n=3的情形。
多元微分学
一元函数微分学到多元函数的扩展。
连续性设在同一个过程中，变量u随着变量x和y而变化，就称u为x和y的一个函数，记为
。
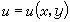这时 u的数值（的大小）便依赖于x和y的数值(的大小)，把它记为ƒ(x，y)，其中ƒ表示该依赖关系，即函数关系。这函数关系于是又表现为一个数量等式
。
这有序数组(x，y)在一个平面直角坐标系中代表一个动点P，它的全部可能的位置形成一个平面点集S。从而函数关系ƒ 便把动点P的每一个位置(x，y)对应到变量u的一个惟一确定的数值（函数值）ƒ(x，y)=ƒ(P)。于是整个函数便表现为变量u按照这个对应关系随着动点P在定义域S上变化而变化：
。 (1)
这样，二元函数的概念便同一元函数的一致。
如图1
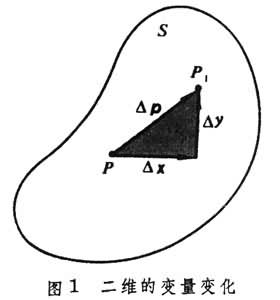
，当动点P由一个位置 P(x，y)变到另一个位置P1(x1y1)时，这变化由它的位移向量
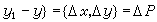来刻画，这变化的大小便由这向量的长度
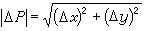来度量。相应的u的变化
，其大小由|Δu|来度量。于是多元函数(1)在一点P 处的连续性也同一元函数的一致，即在P1无限趋近于P的过程中，｜Δu｜随着｜ΔP｜而无限变小。这就是说，对于每一个正数ε都存在一个正数δ使得
。 (2)
这导致多元连续函数的基本性质也同一元连续函数的一样：在一有界闭集 S上处处连续的一个函数至少在某一点处达到最小值m，又至少在某一点处达到最大值M；其连续性在整个集合 S上是一致的（即(2)中的δ不依赖于P而对于S上的每个点P都有效）；并且，如果S是连通的（即S上每两点都能够用完全位于S上的一条折线连接起来）， 则每一个中间值μ(m≤μ≤M)都是某一点处的函数值。
函数(1)的连续性，作为一个局部性质，它在S的每个内点处都可以分解成一元的情形。如图2
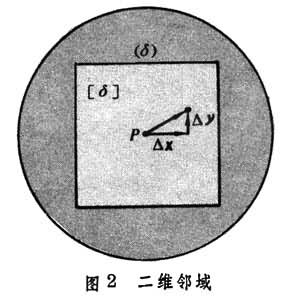
，只要函数(1)在一点P的某个领域(δ)内处处连续，则（根据上述基本性质）必定在其内部的一个方邻域 [δ]上一致连续，而在这个方邻域上的变化量具有图1所启示的向量分解式
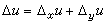， (3)
式中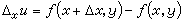
，
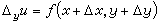
分别作为一元函数
(4)
的变化量，其连续性分别关于y或x+Δx是一致的（即相应于(2)中的δ不依赖于y或x+Δx ）。
偏导数连续性(2)的进一步研究，是要在变化量分解式(3)的基础上，利用一元函数(4)来阐明，在｜ΔP｜趋向0的过程中，变化量Δu随 Δx、Δy趋向0的依赖关系。这就要用到一元函数(4)的变化率，即导数g
(x)、h(y)。假定它们在P(x，y)的附近都存在，并分别记为ƒ
(x，y)。ƒ
(x+Δx，y)通常也写成
这种对自变量之一(其余作为参变量)的导数称为偏导数。利用这些偏导数的存在和一元微分学的中值定理，可以把(3)写成
，
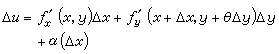式中θ介于0到1之间，α为无限小量。当偏导数 ƒ
连续时，可以进一步写成
， (5)
α、β为无限小量。
全微分分解式(5)表明，在点P 处，变化量 Δu随着Δx、Δy 趋向0的过程中，存在着近似线性的依赖关系
， (6)
式中主要部分的系数A、B不依赖于 Δx、Δy，而余项部分的系数α、β是无限小量。对此我们说函数u在点P处是可微的，并称这个线性主要部分为u的一个(全)微分，且记为
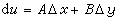。 (7)
但在关系(6)中令Δx→0，Δy＝0或Δx＝0，Δy→0，即可推出
所以只要微分存在，它的系数就必然是偏导数，因而是惟一的。然而，在某些特殊情形，这些偏导数都存在，关系(6)却不成立；所以，不同于一元函数的情形，只有偏导数的存在还不能保证微分存在。
不过，公式(6)的推导已经表明，这些偏导数的连续性可以保证微分存在。这时就说函数是连续可微的。最基本的连续可微函数就是自变量本身作为 P=(x，y)的函数：
。 (8)
这时 dx＝1·Δx＋0·Δy＝Δx，dy＝0·Δx＋1·Δy＝Δy。因此u的微分可以写成
。 (9)
这样，微分的定义等式(7)就由微分与差分的关系变成了纯粹是微分之间的关系。这微分关系式 (9)以相同的线性系数代表着差分的近似关系(5)，并成为分解式(3)的分解过程的完成形式，微分形式。
变量替换在微分形式(9)中，变量x、y既然当作动点P的函数，如(8)所示，它们也就是动点P在任一别的坐标系(r，s)中的坐标的函数：
。 (10)
假定这些坐标函数也在其定义域S┡上是处处连续可微的，也就是说，出现在下列微分等式中的系数都是连续的：
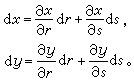(11)
既然u关于(x，y)连续可微，公式 (5)便给出偏导数的连锁法则：
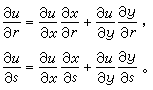(12)
这些偏导数都是关于新变量 (r，s)连续可微的函数。于是u也关于(r，s)连续可微，因而结合(12)与(11)便得到
。
这表明微分形式(9)对于x，y为任何连续可微的函数都成立。这称为（一阶）微分的形式不变性。
变量替换(10)规定了一个坐标平面上的动点P(x，y)随着另一坐标平面上的动点Q(r，s)而变动，因而定义了一个函数T:P=T(Q)。这样，函数组(10)便被表示成一个函数。它经过微分转化成的线性（微分）方程组(11)可以缩写成一个矩阵方程
。
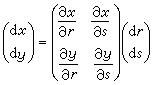这里，偏导数所形成的矩阵称为雅可比矩阵。它是微分向量的系数矩阵，相当于一元函数情形的微分系数或导数，有时记为T┡。它的行列式称为雅可比行列式，常记为
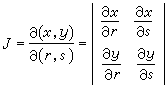。 (13)
当J ≠0 时，便意味着以它为系数行列式的微分方程组(11)和(12)都是可解的；而隐函数存在定理则在于断言，这时函数方程组(10)也是可解的，即至少在相应的一对点P、Q的附近存在着反函数Q=T-1(P)，它也是连续可微的，其微分便是(11)的解。于是，在这两个点的邻域内，两种坐标之间存在着连续可微的一一对应关系（x，y）凮（r，s）。
如果(8)中的动点 P是在一个三维坐标空间(r，s，t)中，则(10)中的函数应是三元的：
。
这不影响微分形式不变性。缩写式仍是 P＝T(Q)。这里，雅可比矩阵则是
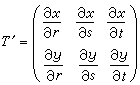(14)
而雅可比行列式则是二阶余子式：
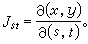
这些雅可比行列式相当于T的偏导数。
多元积分学
一元函数积分学到多元函数的扩展。
重积分一元函数的定积分，作为黎曼积分和的极限，推广到二元函数(1)几乎是直接的。这里，积分区间，作为自变量的变化范围，换成了两个区间X(α≤x≤A)和Y(b≤y≤B)，它们的乘积R=X×Y是包含有界闭区域S的（各边平行于坐标轴的）最小的矩形（图3
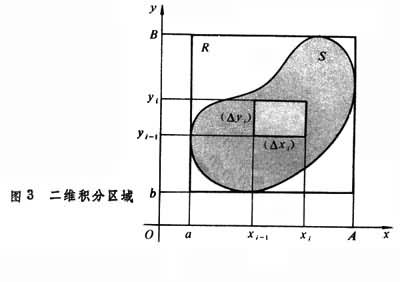
）。对于R上不属于S的点，取函数值为0，并仿照一元的情形作黎曼和数
。
分划(Δ)的细密程度由全部Δxi，Δyj的最大值‖Δ‖来度量。于是，可以像一元的情形一样来定义二重积分
。
如果这个极限存在，就说函数ƒ在区域S上是可积的。可积的一个充分必要条件仍然是，函数有界并且几乎处处连续（即不连续点形成一个零测度集合）。不过，这里的零测度集合，作为平面上的点集，是指能用总面积任意小的矩形序列覆盖住。
在可积的前提下，二重积分可以写成
， (15)
内层积分以y为参变量，在不可积（因而相应的y值形成一个一维零测度集合）时算作0。
面积微分dR=dxdy，作为一个微小矩形的面积，在坐标变换(10)之下由这变换的微分形式(11)来确定，成为一个以向量
和 
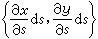为一对邻边的平行四边形的面积，即行列式
的绝对值：
。
这导致二重积分的换元公式
。 (16)
二重积分，作为关于面积微分的一种求和过程，可以推广到空间中的一块曲面S上，只要这曲面是光滑的，即其上的动点P(x，y，z)的坐标能够表示成某一平面矩形S
=(α≤r≤A)×(b≤s≤B)上的连续可微的函数，而以(r，s)作为P的一种新的坐标（曲面坐标）。这里 S的微小矩形（Δr）×（Δs）对应着 S上的微小曲面四边形 ΔS，后者的面积关于前者的面积 ΔrΔs 的线性主要部分便是曲面的面积微分dS。它等于以切线向量
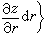和
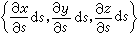为一对邻边的平行四边形的面积：
，
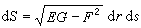式中
，
。
。
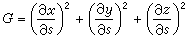从而面积分能够表示成二重积分：
。 (17)
曲面S可以是逐片光滑的，积分便取为各片上的积分之和。
线积分如果我们类似地考虑空间中一条光滑的(或逐段光滑的)曲线C上关于弧长的微分ds的积分
，
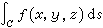则有类似于(17)的结果：
但其实这种(第一型) 线积分本身就只是一个直线段0≤s≤l上的一类通常的定积分（不考虑积分区间的定向）。如果我们考虑关于弧长微分ds的向量形式｛dx，dy，dz｝的积分
，
则这种（第二型）线积分是定积分的推广。它可以写成第一型的形式：
， (19)
(这表明它是函数向量｛u，v，w｝在切线方向上的投影的第一型线积分。但它原来的形式更直接地表现着作为全微分的逆运算的性质。
公式(15)～(19)表明，定积分在概念上的各种推广，在计算上仍都能回到定积分。
基本公式定积分，作为微分之逆，到各种积分的推广，导致这互逆关系的基本公式(牛顿-莱布尼茨公式)的推广。这公式的意义在于，函数的导数经过积分运算之后，便消去导数中所含的微分运算而返回到原来函数的差分，起着化简的作用。我们现在先考虑嬠w/嬠z，积分区域取为一个椭球体V。用R 表示V 在 xy平面上的垂直投影，S1和 S0表示上下边
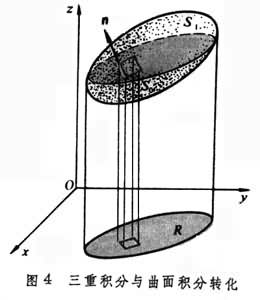
界面，S 表示全部边界面，
表示其单位外法向量（图4）。如果这偏导数在V 上处处存在并且可积，则其三重积分可以像二重积分(15)那样分解，然后通过牛顿-莱布尼茨公式转化为边界S上的曲面积分：
一般地，对于一块逐片光滑的曲面S所围成的三维区域V有
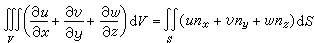， (20)
只要所含三个偏导数都在V上处处存在并且可积。
取V=S0×(0，1)，u=u(x，y)，υ =υ(x，y)，w=0，这公式就化成二维空间中的奥氏公式：
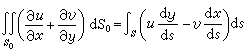， (21)
其中曲线s，作为平面区域S0的全部边界，是逐段光滑的，它的切线的定向｛dx，dy｝到S0的外法线｛dy，-dx｝的旋转方向同正y轴到正x轴的一致。这个（法线形式的）曲线积分通常简记为（切线形式）
，
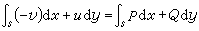从而(21)可以改变形式成为
格林公式：
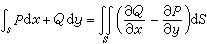， (22)
由此能够证得三维空间中的格林公式，亦即斯托克斯公式：
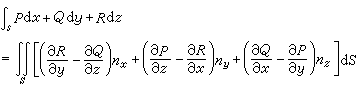(23)
其中逐段光滑曲线s是逐片光滑曲面S的全部边界，二者的定向是协调的。这意思是：S 的单位法向量 
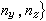在组成S的每一光滑片段上是随起点(x，y，z)而连续变动的，它到这片区域的外法向量、再到边界曲线的切线向量所构成的螺旋转向同正z轴到正x轴、再到正y轴的螺旋转向是一致的，并且任何相邻两片段的定向在边界曲线的公共部分上是相反（相消）的。
由这个公式推知，在开区域V内，若要一个带连续系数的微分式Pdx+Qdy+Rdz恰好是某一函数的全微分，就必须它的系数满足恒等式
只要这些偏导数都是连续的。反之，当这些偏导数都是连续的并且满足这些恒等式时，在V的每一个（曲面）单连通的有界部分区域V1（意即在其内的每一条光滑的简单闭曲线都有一块以它为全部边界的光滑闭曲面）内都存在一个函数U，它的全微分 dU恰好就是原来的微分式Pdx+Qdy+Rdz。于是，在V1内，对于每一条逐段光滑的曲线 A …B 都有
(24)
这样，牛顿-莱布尼茨公式就随着积分概念经过各种推广(20)～(24)之后，仍回到了它原来的形式。
历史上，多元微积分学的基本概念都是在微分与积分的基本思想的应用中，与一元函数的合为一体，适应描述和分析物理现象和规律的需要而产生的。偏导数、重积分的朴素思想（I.牛顿，1687），二重积分及其累次积分与换元计算方法（L.欧拉，1769），三重积分及其累次积分与换元计算方法（J.-L.拉格朗日，1773）都是初期出现在力学研究的著作中，并不是有意识地要建立相关的数学理论。牛顿-莱布尼茨公式的两种形式(20)和(21)都延迟了一个时期才明确出现在热传导和电磁的研究中（M.B.奥斯特罗格拉茨基，1828；G.格林，1828），且是作为物理定理来理解的。变量替换中的雅可比行列式也延迟到微积分的理论分析开展起来以后，才获得明确的概念和系统的研究（C.G.J.雅可比1833、1841，奥斯特罗格拉茨基1834），而变量替换中隐含着的曲线坐标则同时延迟到热传导和电磁的研究中问题求解的需要和物理意义的启示达到相当明朗的程度，才获得明确的概念和系统的研究（G.拉梅1833、1859）。只有斯托克斯公式是作为格林公式的理论应用来叙述的（L.开尔文，1850；G.G.斯托克斯，1854）。不过这时微积分学已由于它的理论分析的发展而成为一门自立的学科了。
总的说来，多元微积分学是在微积分的基本思想的应用和发展中自然地、水到渠成般地形成起来的。